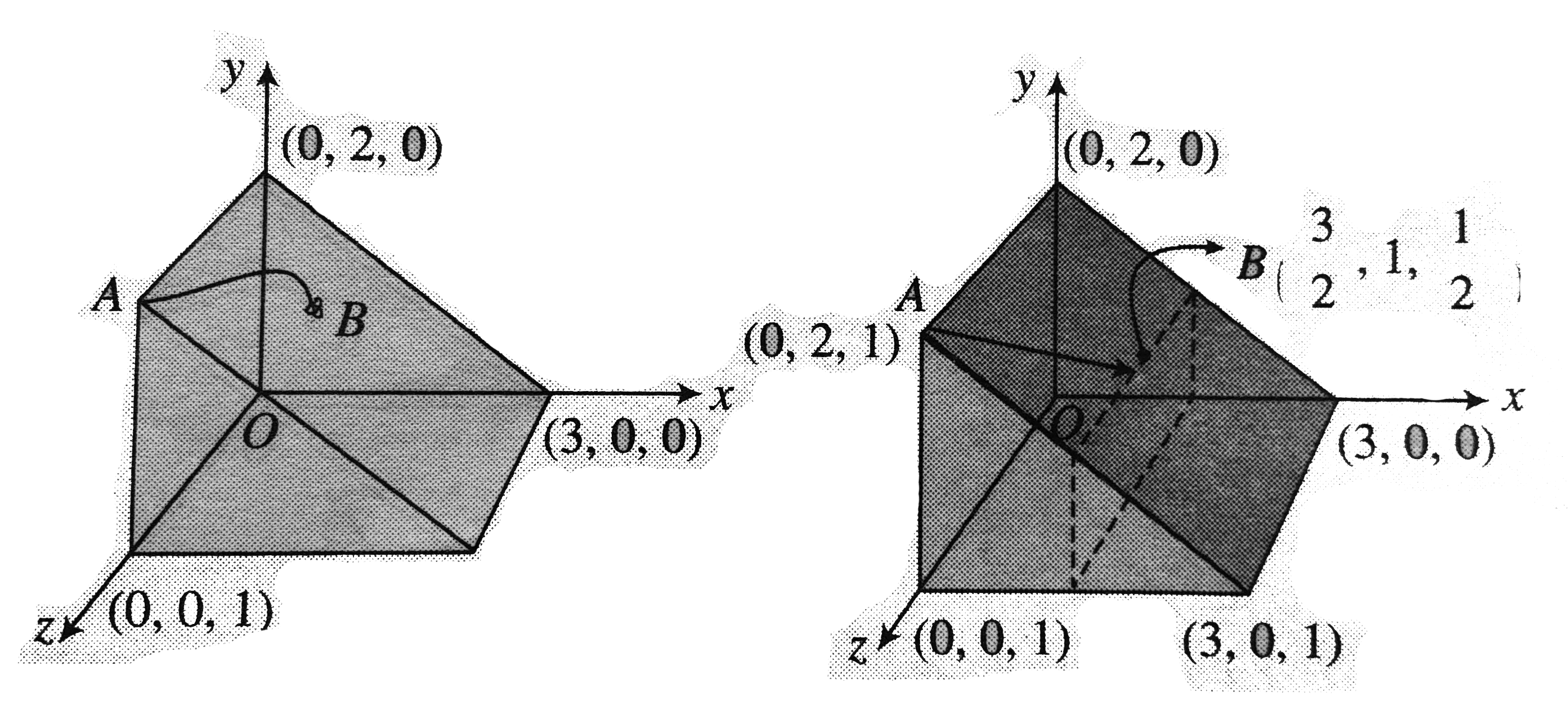
An insect crawls from A to B where B is the centre of the rectangular slant face. Find the (a) initial and final position vector of the insect and (b) displacement vector of the insect.
 .
.
Initial position vector of insect
−−→OA=2ˆj+ˆk(m)
−−→OB=32ˆi+ˆj+12ˆk(m)
Displacement of insect −−→AB= position vector of →B-position vector of →A.
−−→AB=(32−0)ˆi+(1−2)ˆj+(12−1)ˆk=32ˆi−ˆj−12ˆk(m)
Hence, magnitude of displacement
∣∣∣−−→AB∣∣∣=√(32)2+(1)2+(12)2=√94+1+14=√72m.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Knowledge Check
If a and b are position vector of two points A,B and C divides AB in ratio 2:1, then position vector of C is
Aa+2b3B2a+b3Ca+23Da+b2Which of the following Statement(s) is/are correct?
I. To find displacement of an object in two-dimensional motion, we need initial and final positions.
II. There is no relation between the positions and displacement vectors. Choose the correct statements for the given statements.AOnly statement I Is correctBOnly statement II is correctCBoth the statements are correctDBoth the statements are incorrectIf a,b and c are the position vectors of the vertices A,B and C of the ΔABC, then the centroid of ΔABC is
Aa+b+c3B12(a+b+c2)Ca+b+c2Da+b+c2
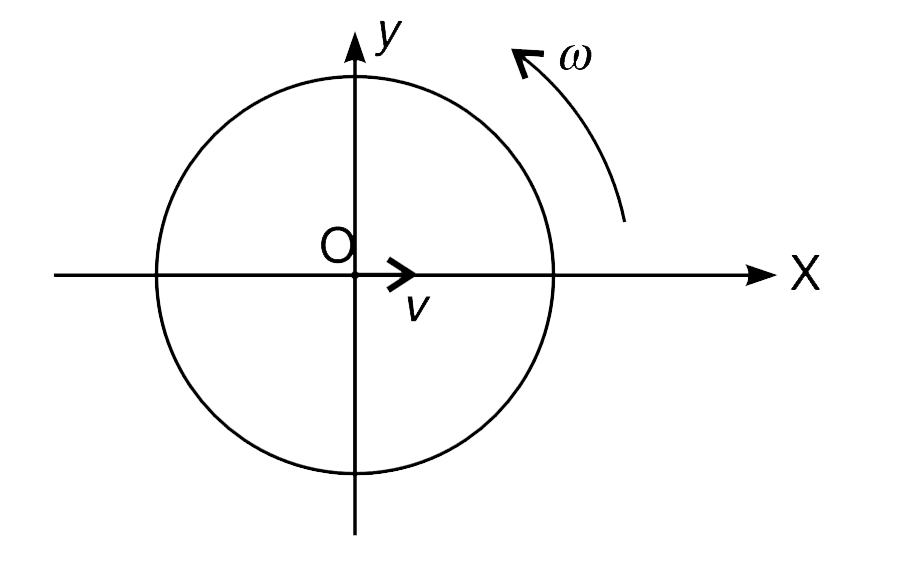
A disc is rotating with constant angular velocity ω in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t=0 with a constant speed V relative to the disc. At time t=0 the velocity of the insect is along the X direction.
(a) Write the position vector (→r) of the insect at time ‘t’.
(b) Write the velocity vector (→v) of the insect at time ‘t’.
(c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle θ given by tanθ=1θ.
View SolutionIf →aand→b are position vectors of points AandB respectively, then find the position vector of points of trisection of AB .
View SolutionA uniform bar AB of length 6a has been placed on a horizontal smooth table of width 5 a as shown in the figure. Length 2a of the bar is overhanging. Mass of the bar is 4m. An insect of mass m is sitting at the end A of the bar. The insect walks along the length of the bar to reach its other end B.
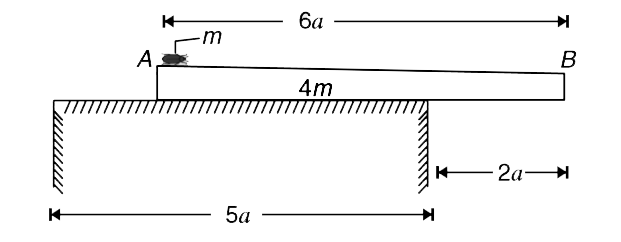
(a) Will the bar topple when the insect reaches end B of the bar ?
(b) After the insect reaches at B, another insect of mass M lands on the end A of the bar. Find the largest value of M which will not topple the bar.
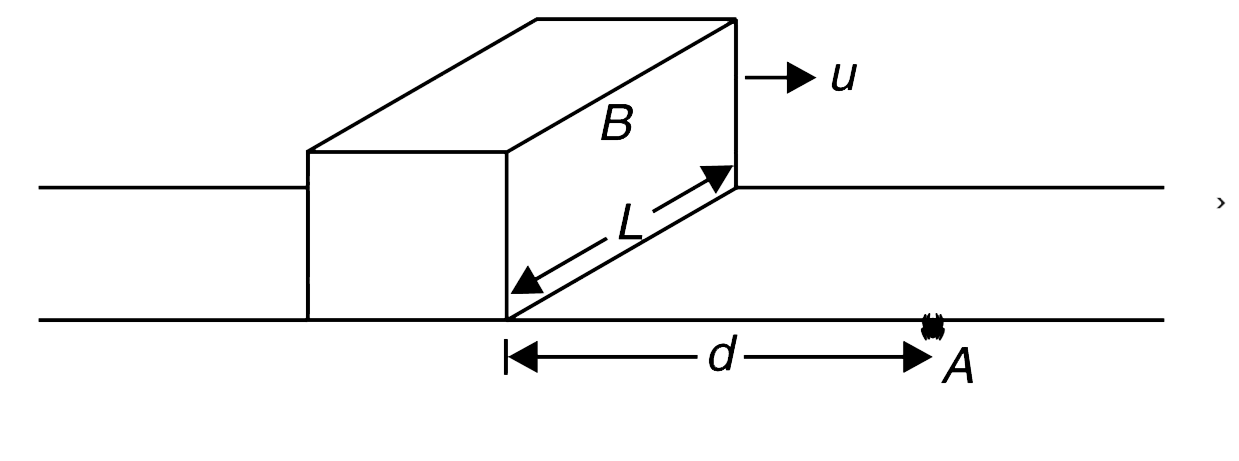
View SolutionA heavy block 'B' is sliding with constant velocity u on a horizontal table. The width of the block is L. There is an insect A at a distance d from the block as shown in the figure. The insect wants to cross to the opposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v for which the insect can cross to the other side without getting hit by the block.
View SolutionThree points with position vectors, a, b, c are collinear if
View Solution
