An LR circuit with emf ε is connected at t = 0. (a) find the charge Q which flows through the battery during O to t. (b) Calculate the work done by the battery during this period. (d) find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with enegy conservation.Solution in Gujrati
(a)(dq)=
=i0(1−e−t/(τ))dt
=i0(1−e−t/(τ))dt[∴(τ)=(LR)]
Q=int_(0)^(t) (dq)<br>=i_(0)[int_(0)^(t)(dt)-int_(0)^(t)(e^(-(tR)//L)(dt)]<br>i_(0)[t-(L/R)(1-(e^(-(tR)//L))]<br>i_(0)[t-(-(L)/(R))(1-(e^(-(tR)//L))]_(0)^(t)<br>Q=(E/R)[t-((L)/(R))(1-(e^(-(tR)//L))]<br>(b)similarlyasweknowworkdo≠<br>=Vl=Ei
Ei0[t−(LR)(1−(e−(tR)/L))]
=E2R[t−(LR)(1−(e−(tR)/L)]
(c) H=∫t0(i2)(R).(dt)
=E2R2.R.∫t0(1−(e−(tR)/L)2.(dt)
E2R∫t0(1−(e−(2tR)/L)−2e−(tR)/L)(dt)]
E2R(t−L2Re−2tR/L+LR2.(e−(tR)/L))t0
E2R(t−L2Re−2tR/L+LR2.(e−(tR)/L))
−(−L2R+2LR)
E2R{t−L2R(x2−4x+3)}
[wherex=e−tR/L]
(d) E=(12)Li2=12(L)(E2R2(1−(e−(tR)/L))2
(LE)22R2(1−x)2
[wherex=(e−(tR)/L)]
(e) Total energy stored in magnetic field
E2Rt−E2LR2(e−(tR)/L)
E2R{t−L2R(1−x)}
=Energy drawn from battery.
(Hence conservation of energy hold good).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
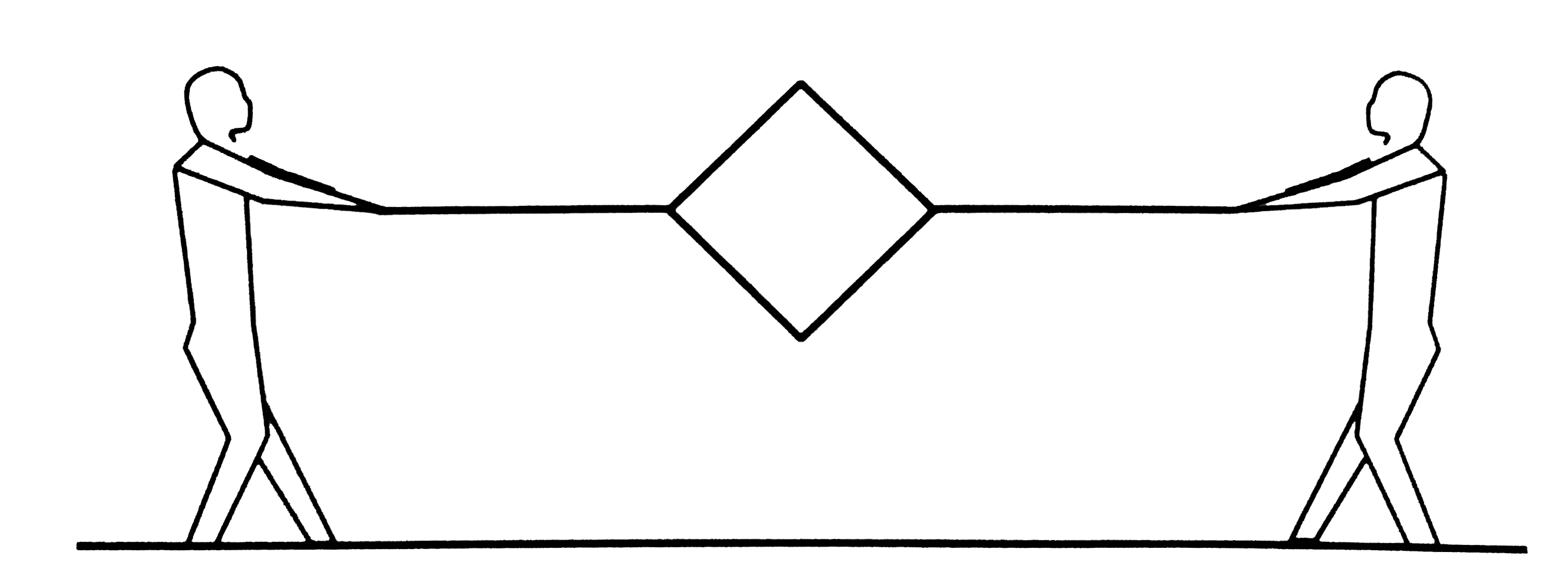
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionAn LR circuit with emf ε is connected at t = 0. (a) find the charge Q which flows through the battery during O to t. (b) Calculate the work done by the battery during this period. (d) find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.
View SolutionA capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf epsilon . Find the heat dissipated in the circuit during the process of charging .
View SolutionA simple LR circuit is connected to a battery at time t = 0 . The energy stored in the inductor reaches half its maximum value at time
View SolutionConsider a circuit consists of resistors, inductor, battery and a switch as shown. Resistance of resistors, inductance of inductor and EMF of battery are indicated. The switch is closed at t=0.

Find time constant of LR circuit during growth of current
View SolutionAn LR series circuit with a battery is connected at t=0. Which of the following quantities are zero just after the connection?
View SolutionThe figure below shows a battery of emf epsilon connected to an inductor L and resistance R in series. If the switch is closed at t=0, then the total charge that flows from the battery in time constant of the circuit is
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionAn inductor-resistance -battery circuit is switched on at t = 0. find the emf of the battery in one time constant .
View SolutionAn LR circuit with a battery is connected at t=0. Which of the following quantities is not zero just after the connection?
View SolutionA circuit contains an inductor of value 2H as shown at t=0 no current was flowing through battery. Find the energy stored in inductor at t=4 sec.

View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View Solution
