An object is in unifrom motion along a straight line . What will be position-time graph for themotion of the object if
(a) x0=+ve,v=+ve(b)x0=+ve,v=−ve(c)x_(0) =- ve, v= + ve and (d) both x0 and v are negative ? The letters x0 and v position of theobject at time t=0 and vrepresentposituionoftheobjectattimet=0 and uniform velocity of theobject respectively.
To solve the problem of determining the position-time graph for an object in uniform motion under different conditions of initial position x0 and velocity v, we need to analyze each case step by step.
1. Understanding the Position-Time Equation:
The position of an object at time t can be described by the equation:
x(t)=x0+vt
where x0 is the initial position and v is the uniform velocity.
2. Case (a): x0>0, v>0:
- Here, both the initial position and velocity are positive.
- The object starts at a positive position and moves in the positive direction.
- The graph will be a straight line with a positive slope.
- Graph: Starts above the origin and slopes upwards.
3. Case (b): x0>0, v<0:
- The initial position is positive, but the velocity is negative.
- The object starts at a positive position and moves in the negative direction.
- The graph will be a straight line with a negative slope.
- Graph: Starts above the origin and slopes downwards.
4. Case (c): x0<0, v>0:
- The initial position is negative, but the velocity is positive.
- The object starts at a negative position and moves in the positive direction.
- The graph will be a straight line with a positive slope.
- Graph: Starts below the origin and slopes upwards.
5. Case (d): x0<0, v<0:
- Both the initial position and velocity are negative.
- The object starts at a negative position and moves further in the negative direction.
- The graph will be a straight line with a negative slope.
- Graph: Starts below the origin and slopes downwards.
Summary of Graphs:
- (a): Positive initial position and positive velocity → Upward sloping line starting above the origin.
- (b): Positive initial position and negative velocity → Downward sloping line starting above the origin.
- (c): Negative initial position and positive velocity → Upward sloping line starting below the origin.
- (d): Negative initial position and negative velocity → Downward sloping line starting below the origin.
The position of an object at time t can be described by the equation:
x(t)=x0+vt
where x0 is the initial position and v is the uniform velocity.
- Here, both the initial position and velocity are positive.
- The object starts at a positive position and moves in the positive direction.
- The graph will be a straight line with a positive slope.
- Graph: Starts above the origin and slopes upwards.
- The initial position is positive, but the velocity is negative.
- The object starts at a positive position and moves in the negative direction.
- The graph will be a straight line with a negative slope.
- Graph: Starts above the origin and slopes downwards.
- The initial position is negative, but the velocity is positive.
- The object starts at a negative position and moves in the positive direction.
- The graph will be a straight line with a positive slope.
- Graph: Starts below the origin and slopes upwards.
- Both the initial position and velocity are negative.
- The object starts at a negative position and moves further in the negative direction.
- The graph will be a straight line with a negative slope.
- Graph: Starts below the origin and slopes downwards.
- (a): Positive initial position and positive velocity → Upward sloping line starting above the origin.
- (b): Positive initial position and negative velocity → Downward sloping line starting above the origin.
- (c): Negative initial position and positive velocity → Upward sloping line starting below the origin.
- (d): Negative initial position and negative velocity → Downward sloping line starting below the origin.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Con ceptual Problems15videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Con ceptual Problems27videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Conceptual Problems2videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
An object is in unifrom motion along a straight line . What will be position-time graph for themotion of the object if
(a) x0=+ve,v=+ve (b) x0=+ve,v=−ve(c)x_(0) =- ve, v= + veand(d)⊥hx_(0) and v are negative ? The letters x0 and v position of theobject at time t=0 and v represent posituion of the object at time t=0 and uniform velocity of theobject respectively.View SolutionAn object is in unifrom motion along a straight line . What will be position-time graph for themotion of the object if
(a) x0=+ve,v=+ve (b) x0=+ve,v=−ve(c)x_(0) =- ve, v= + veand(d)⊥hx_(0) and v are negative ? The letters x0 and v position of theobject at time t=0 and v represent posituion of the object at time t=0 and uniform velocity of theobject respectively.View Solution
Knowledge Check
- Question 1 - Select One
Observe the following compound and select +ve & −ve test respectively.
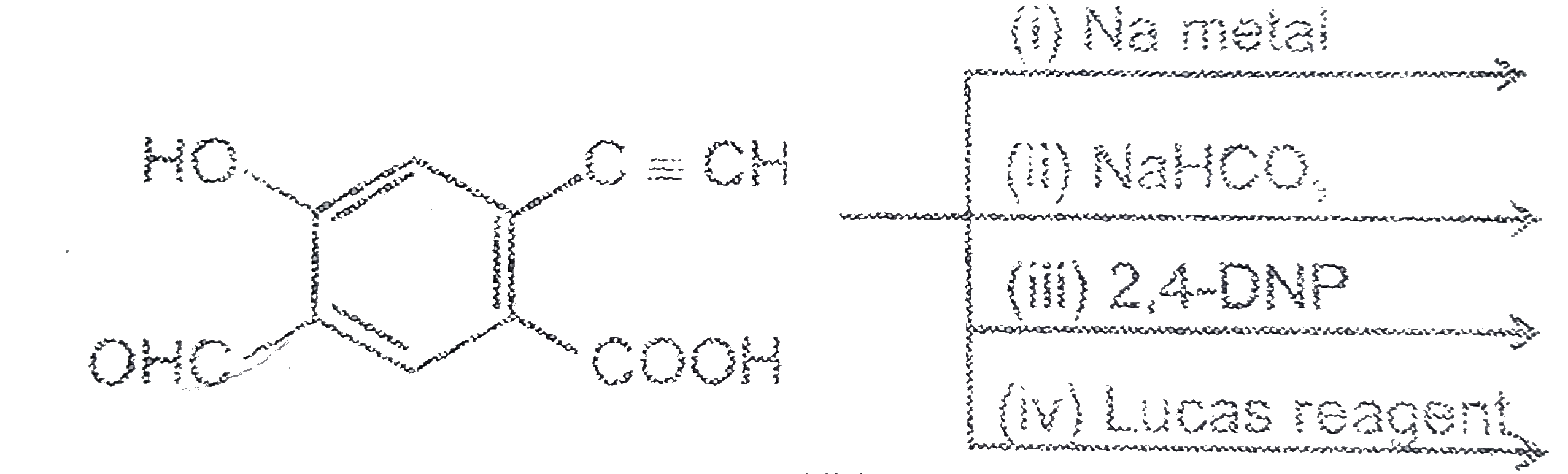 A+++−B++++C+−+−D+−−+
A+++−B++++C+−+−D+−−+ - Question 2 - Select One
Observe the following compound and select +ve & -ve test respectively
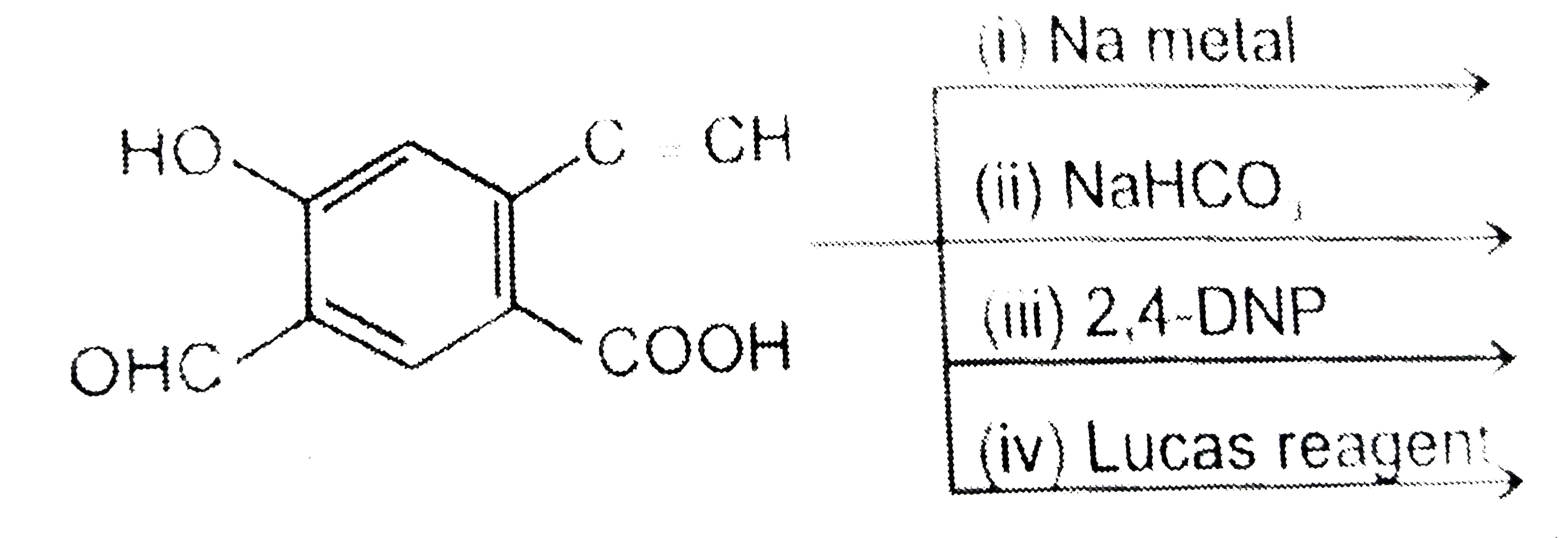 A+++−B++++C+−+−D+−−+
A+++−B++++C+−+−D+−−+ - Question 3 - Select One
The position of a particle at time t is given by the relation x(t)=v0A(1−e−At), where v0 is constant and A>0. The dimensions of v0 and A respectively
A[M0LT0] and [T−1]B[M0LT−1] and [T−2]C[M0LT−1] and [T]D[M0LT−1] and [T−1]
An object is in unifrom motion along a straight line . What will be position-time graph for themotion of the object if
(a) x0=+ve,v=+ve (b) x0=+ve,v=−ve(c)x_(0) =- ve, v= + veand(d)⊥hx_(0) and v are negative ? The letters x0 and v position of theobject at time t=0 and v represent posituion of the object at time t=0 and uniform velocity of theobject respectively.View SolutionAn object is in unifrom motion along a straight line . What will be position-time graph for themotion of the object if
(a) x0=+ve,v=+ve (b) x0=+ve,v=−ve(c)x_(0) =- ve, v= + veand(d)⊥hx_(0) and v are negative ? The letters x0 and v position of theobject at time t=0 and v represent posituion of the object at time t=0 and uniform velocity of theobject respectively.View SolutionAn object is moving along +ve x-axis with a uniform acceleration of 4ms−2 . At time t=0 , x=5m and v=3ms−1 .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of 5ms−1?View SolutionAn object is moving along+ve x-axis with a uniform acceleration of 4 ms^(-2).Attime t=0.X=4m and v=2ms−1.<br>(a)Wˆwillbethevelocityandpositionoftheobjectattime t=3 s?
(b) What will be the position of the object when it has a velocity 8ms−1 ?View SolutionFind the average velocity of a particle moving along a straight line such that its velocity changes with time as v(m/s)=4sin.π2t, over the time interval t=0 to t=(2n−1)2 seconds. (n being any + ve integer).
View Solution

