An object is placed in front of a converging lens at a distance equal to twice the focal length f1 of the lens. On the other side of the lens is a concave mirror of focal length f2 separated from the lens is a concave mirror of focal length f2 separated from the lens by a distance 2(f1+f2). Light from the object passes rightward through the lens, reflects from the mirror, passes leftward throught the lens, and forms a final image of the object.

The distance between the lens and the final image is equal to 2f1.
The distance between the lens and the final image is equal to 2(f1+f2)
The final image is real, inverted and of same size as that fo the object.
The final image is real, erect and of same size as that of the object.
The correct Answer is:a,c.
I1 is image of O through lens.
I2 is image of I1 through mirror.
I3 is image of I2 through lens.
I3 is of same size of O and inverted w.r.t. O.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
Consider a transparent hemispher (n=2) in front of which a small object is placed in air (n=1) as shown in figure.
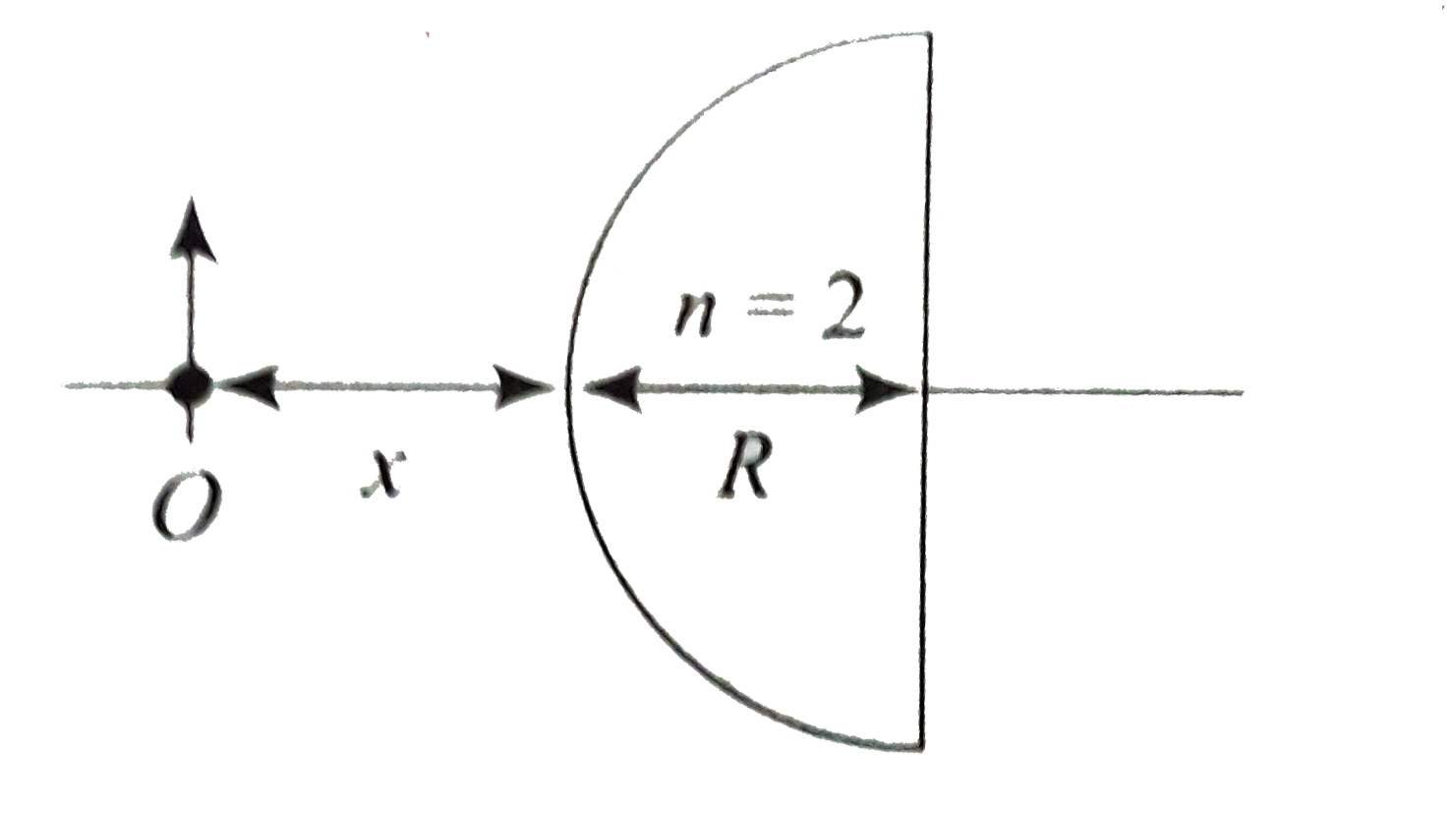
Q. For which value of x, of the following , will the final image of the object O be virtual?06:26View SolutionConsider a transparent hemisphere (n=2) in front of which a small object is placed in air (n=1) as shown in figure.
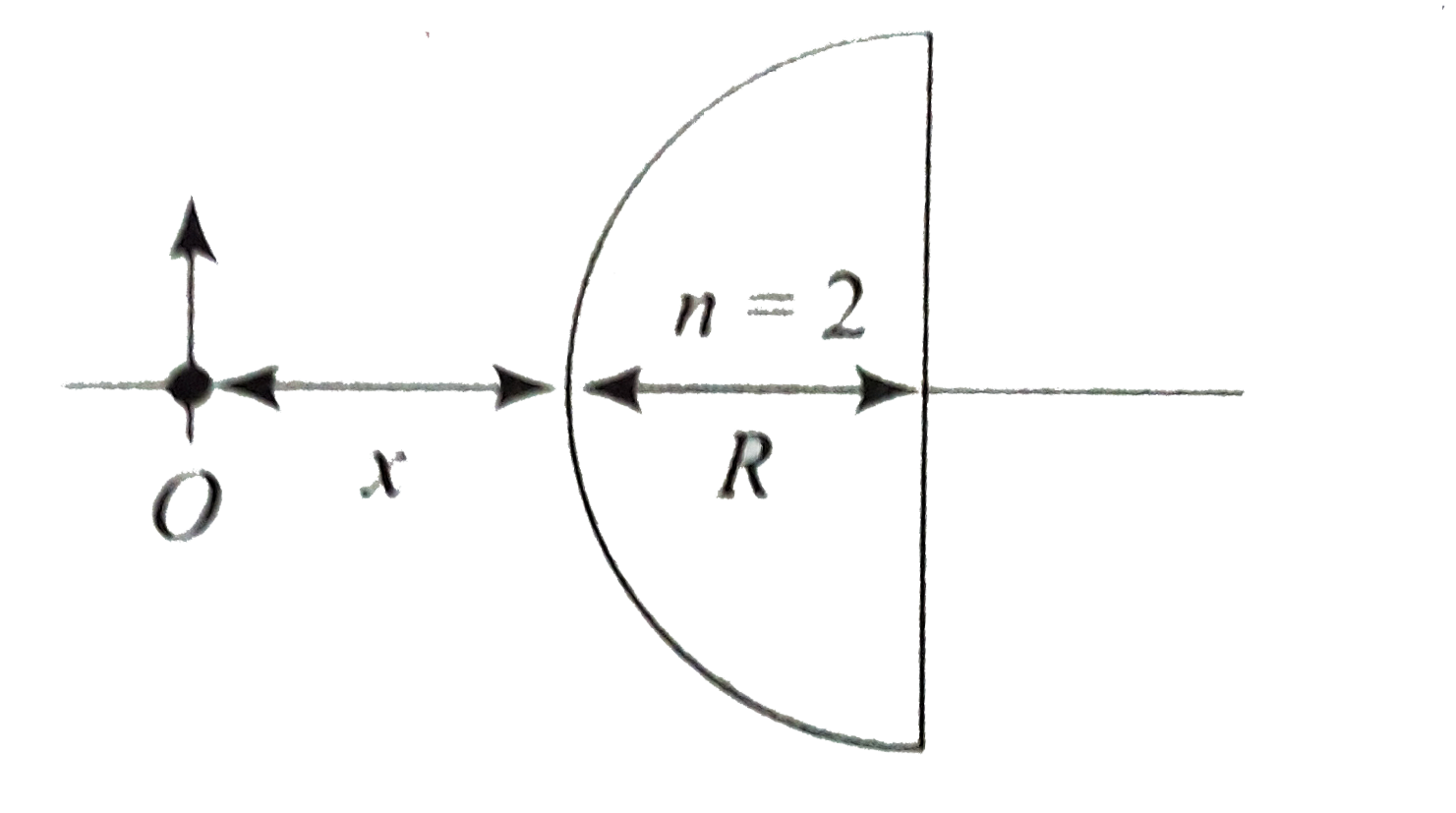
Q. Consider a ray starting from O which strikes the spherical surface at grazing incident (i=90∘). Takin x=R, what will be the angle (from normal) at which the ray may emerge from the plane surface.04:56View SolutionA ray of light is falling on a glass sphere of μ=√3 such that the incident ray and that the incident ray and the emergent ray, when produced, intersect at a point on the surface of the sphere. Find the value of angle of incidence( in degree).
03:54View SolutionA rope of length L and mass M is being pulled on a rough horizontal floor by a constant horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rope. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rope is
04:17View SolutionA body weighs W newton at the surface of the earth. Its weight at a height equal to half the radius of the earth will be kW9. Find k.
02:07View SolutionA diverging lens of focal length f1 is placed in front of and coaxially with a concave mirror of foacl length f2. Their separation is d. A parallel beam of light incident on the lens returns as a parallel beam from the arrangement. Then,
01:02View SolutionA converging lens of focal length f_(1) is placed in front of and coaxially with a convex mirror of focal length f_(2) . Their separation is d. A parallel beam of light incident on the lens returns as a parallel beam from the arrangement, Then,
02:48View SolutionLet f_(v) and f_(r) are the focal lengths of a convex lens for violet and red lights respectively. If F_(v) and F_(r) are the focal lengths of a concave lens for violet and red light respectively, then
01:55View SolutionA concave mirrorr of focal length f_(1) is placed at a distance of d from a convex lens of focal length f_(2) . A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
02:44View SolutionWe combined a convex lens of focal length f1 and concave lens of focal lengths f2 and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
01:38View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
03:47View SolutionA biconvex lens of focal length f_(1)=10cm is placed 40 cm in front of a concave mirror of focal length f_(2)=7.50 cm, as shown in the figure. An object, 2 cm high, is placed 20 cm to the left of the lens. The image formed by the lens, as rays travel to the right, is
02:42View SolutionA convex lens of focal length f_(1) is kept in contact with a concave lens of focal length f_(2) . Find the focal length of the combination.
03:16View SolutionA concave mirrorr of focal length f_(1) is placed at a distance of d from a convex lens of focal length f_(2) . A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
View SolutionWe combined a convex lens of focal length f_(1) and concave lens of focal lengths f_(2) and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
04:18View Solution

