An object is projected upwards with a velocity of 100m/s. It will strike the ground after (approximately)
10sec
20sec
15sec
5sec
The correct Answer is:B
To solve the problem of an object projected upwards with an initial velocity of 100m/s, we need to determine how long it will take for the object to strike the ground after being thrown.
1. Identify the Given Values:
- Initial velocity (u) = 100m/s (upwards)
- Acceleration due to gravity (a) = −10m/s2 (acting downwards)
- Displacement (Δx) = 0 (the object returns to the original launch height)
2. Use the Kinematic Equation:
The kinematic equation we will use is:
Δx=ut+12at2
Substituting the known values:
0=100t+12(−10)t2
3. Simplify the Equation:
This simplifies to:
0=100t−5t2
Rearranging gives:
5t2−100t=0
4. Factor the Equation:
Factoring out t:
t(5t−100)=0
5. Solve for t:
This gives us two solutions:
t=0or5t−100=0
Solving 5t−100=0:
5t=100⇒t=20seconds
6. Conclusion:
The object will strike the ground after approximately 20 seconds.
- Initial velocity (u) = 100m/s (upwards)
- Acceleration due to gravity (a) = −10m/s2 (acting downwards)
- Displacement (Δx) = 0 (the object returns to the original launch height)
The kinematic equation we will use is:
Δx=ut+12at2
Substituting the known values:
0=100t+12(−10)t2
This simplifies to:
0=100t−5t2
Rearranging gives:
5t2−100t=0
Factoring out t:
t(5t−100)=0
This gives us two solutions:
t=0or5t−100=0
Solving 5t−100=0:
5t=100⇒t=20seconds
The object will strike the ground after approximately 20 seconds.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Critical Thinking
Explore 19 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Graphical Questions
Explore 23 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Relative Motion
Explore 13 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:SET
Explore 27 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
Similar Questions
An object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use g=10m/s2.
View SolutionA ball A is dropped from the top of a tower 500m high and at the same instant another ball b is projected upwards with the velocity of 100m/s. after how much time and where the two balls will meet?
View Solution
Knowledge Check
An object is projected upwards with a velocity of 4.9 m/s. It will strike the ground in approximately
A2 sB1 sC1.5 sD0.5 sA body is projected horizontally from the top of a tower with a velocity of 10m/s.If it hits the ground at an angle 45∘, th vertical component of velocity when it hits ground in m/s is
A10√2B5√2C5D10The velocity of a freely falling body when it strikes the ground is directly proportional to the square of the time taken by it to strike the ground. It takes 5 seconds to strike the ground, with a velocity of 10 m/sec. If it strikes the ground with the velocity of 40 m/sec, then for how long would it have travelled ?
A7.5 secB2.5 secC10 secD20 sec
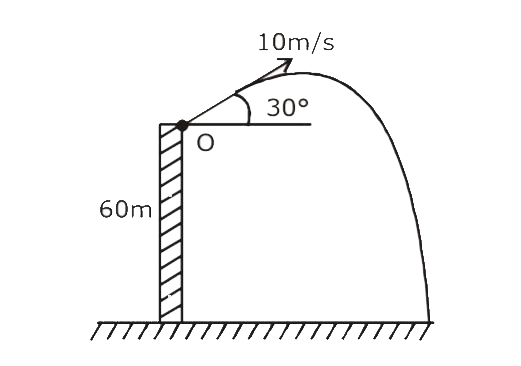
A ball is projected from a point O as shown in figure. It will strike the ground after (g = 10 m/s2)
View SolutionA projectile of mass 50 kg is projected vertically upwards with a velocity of 100 m/s . After 5 seconds it explodes into two pieces , one piece of 20 kg moving vertically upward with velocity 150 m/s . Calculate the velocity of the other piece and also the algebraic sum of the momenta of the system 3 s later .
View SolutionA block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
View SolutionA body X is projected upwards with a velocity of 98ms−1, after 4s, a second body Y is also projected upwards with the same initial velocity . Two bodies will meet after
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View Solution