An object is tied to a string and rotated in a vertical circle of radius r. Constant speed is maintained along the trajectory. If TmaxTmin=2, where, Tmax = maximum tension and Tmin = minimum tension, then v2rg is
1
2
3
4
The correct Answer is:C
At the lowest point, mv2r=TL−mg …(i)
At the highest point, mv2r=TH+mg ….(ii)
As TmaxTmin=TLTH=2∴TL=2TH
As according to question, constant speed is maintained, therefore from equations (i) and (ii), we get
TL−mg=TH+mg or 2TH−mg=TH+mg
or TH=2mg
From equation (ii),
mv2r=3mg or v2rg=3.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)
35 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK YOUR NEET VITALS
25 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (CONSERVATION OF MECHANICAL ENERGY)
17 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
Knowledge Check
A particle is moving in a vertical circle with radius 1 m. It the ratio of TmaxTmin=5 find the velocity at highest point ?
 A5m/sB10m/sC15m/sD20m/s
A5m/sB10m/sC15m/sD20m/sA body of mass m is tied with rope and rotated along horizontal circle of radius r. If T is the tension in the rope and v is the velocity of body and an instant the force required for circular motion is
AT+mv2rBT−mv2rCmv2rDmv24rA particle of mass m is tied to light string and rotated with a speed v along a circular path of radius r. If T=tension in the string and mg= gravitational force on the particle then actual forces acting on the particle are
Amg and T onlyBmg, T and an additional force of mv2/r directed inwardsCmg, T and an additational force of mv2/r directed outwardsDonly a force mv2/r directed outward
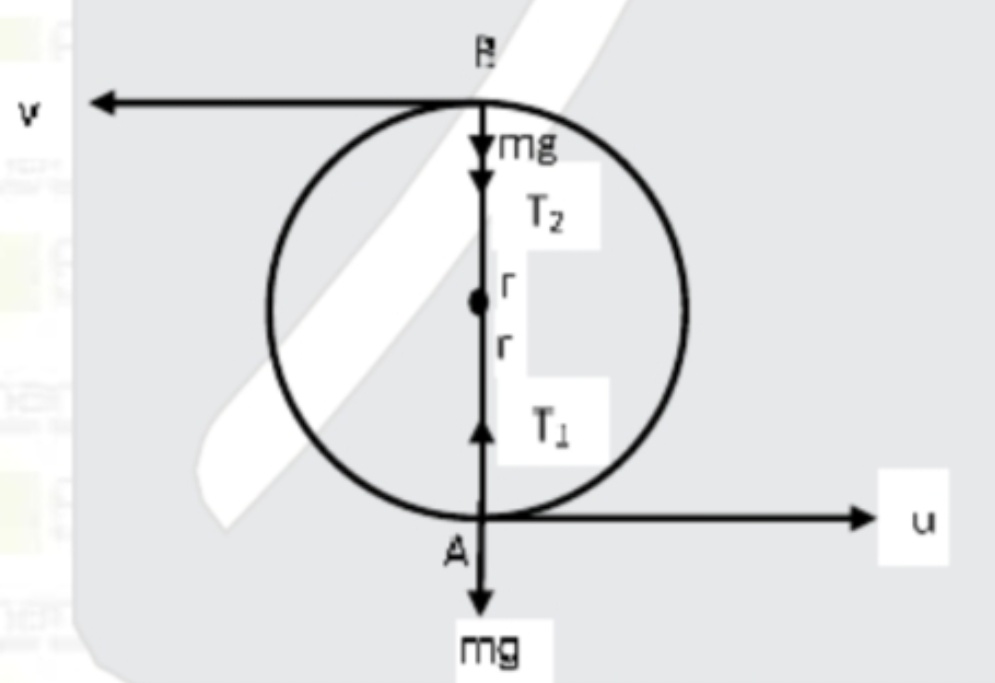
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]

T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.
View SolutionA particle of mass m is tied to light string and rotated with a speed v along a circular path of radius r. If T=tension in the string and mg= gravitational force on the particle then actual forces acting on the particle are
View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionA stone of mass m tied to one end of a string is revolved in a vertical circle of radius R the net forces at the lowest (FL and highest (FH) points of the circle directed vertically downwards are :
(a) FL=mg−T1FH=mg+T2
(b) FL=mg+T1,FH=mg−T2
(c) FL=mg+T1−mυ21R,FH=mg−T2+mυ21R
(d) FL=mg−T1−mυ21R,FH=mg+T2+mυ12R
Choose corret alternative T1,υ1 denote the tension and speed at the lowest point T2,υ2 denote corresponding valuse at the highest point .
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View Solution

