An object moves at a constant speed along a circular path in a horizontal XY plane, with the center at the origin. When the object is at x=−2m, its velocity is −(4m/s)ˆj. What is the object's acceleration when it is y=2m
−(8m/s2)→j
−(8m/s2)→i
−(4m/s2)→j
−(4m/s2)→i
The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the object moving in a circular path and determine its acceleration when it is at a specific position.
Step 1: Understand the motion
The object is moving in a circular path with a constant speed. The center of the circular path is at the origin (0,0) in the XY plane.
Step 2: Identify the given information
- When the object is at x=−2m, its velocity is −4ms in the −j direction (downward).
- We need to find the acceleration when the object is at y=2m.
Step 3: Determine the radius of the circular path
Since the object is at x=−2m, we can find the radius of the circular path. The distance from the center (origin) to this point is:
\( r = \sqrt{(-2)^2 + 0^2} = 2 \text{ m} \)
Step 4: Calculate the speed
The speed of the object is given as 4ms. This speed remains constant as the object moves along the circular path.
Step 5: Use the formula for centripetal acceleration
The formula for centripetal acceleration \( a \) is given by:
\( a = \frac{v^2}{r} \)
where:
- \( v \) is the speed of the object,
- \( r \) is the radius of the circular path.
Step 6: Substitute the known values
Substituting the values we have:
- \( v = 4 \text{ m/s} \)
- \( r = 2 \text{ m} \)
Calculating the acceleration:
\( a = \frac{(4 \text{ m/s})^2}{2 \text{ m}} = \frac{16 \text{ m}^2/\text{s}^2}{2 \text{ m}} = 8 \text{ m/s}^2 \)
Step 7: Determine the direction of acceleration
In circular motion, the acceleration is directed towards the center of the circular path. Since the object is at y=2m, the center is at the origin (0,0), which means the acceleration vector points in the negative j direction (downward).
Step 8: Write the final answer
Thus, the acceleration of the object when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
Final Answer:
The object's acceleration when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
---
The object is moving in a circular path with a constant speed. The center of the circular path is at the origin (0,0) in the XY plane.
- When the object is at x=−2m, its velocity is −4ms in the −j direction (downward).
- We need to find the acceleration when the object is at y=2m.
Since the object is at x=−2m, we can find the radius of the circular path. The distance from the center (origin) to this point is:
\( r = \sqrt{(-2)^2 + 0^2} = 2 \text{ m} \)
The speed of the object is given as 4ms. This speed remains constant as the object moves along the circular path.
The formula for centripetal acceleration \( a \) is given by:
\( a = \frac{v^2}{r} \)
where:
- \( v \) is the speed of the object,
- \( r \) is the radius of the circular path.
Substituting the values we have:
- \( v = 4 \text{ m/s} \)
- \( r = 2 \text{ m} \)
\( a = \frac{(4 \text{ m/s})^2}{2 \text{ m}} = \frac{16 \text{ m}^2/\text{s}^2}{2 \text{ m}} = 8 \text{ m/s}^2 \)
In circular motion, the acceleration is directed towards the center of the circular path. Since the object is at y=2m, the center is at the origin (0,0), which means the acceleration vector points in the negative j direction (downward).
Thus, the acceleration of the object when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
The object's acceleration when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
Topper's Solved these Questions
Similar Questions
An object moves at constant speed along a cicular path in a horizontal xy plane. With the centre as origin.when the object is at x= -2m , it s velocity is −4ˆjm/s , its acceleration when it is at y= 2 m/s
 View Solution
View SolutionAn object moves counter−clockwise along the circular path shown below. As it moves along the path its acceleration vector continuously points towards point S. The object
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass m moves with constant speed in a circular path of radius r under the action of a force of constant magnitude F. the kinetic energy of object is
A12FRBFRC2FRD14FR - Question 2 - Select One
What is the momentum of an object of mass m , moving with a velocityv ?
A(mv)2Bmv2C12mv2Dmv - Question 3 - Select One
When an object is moving with a uniform velocity, what is its acceleration?
ANon-uniformBNegativeCPositiveDzero
A point object moves in + x-direction with v= 1 m/s along the principal axis of the concave mirror of focal length f=10 m. When the mirror moves with a velocity Vm=−ˆi m/s and the object is at a distance of p=15 m, the speed of the image is -
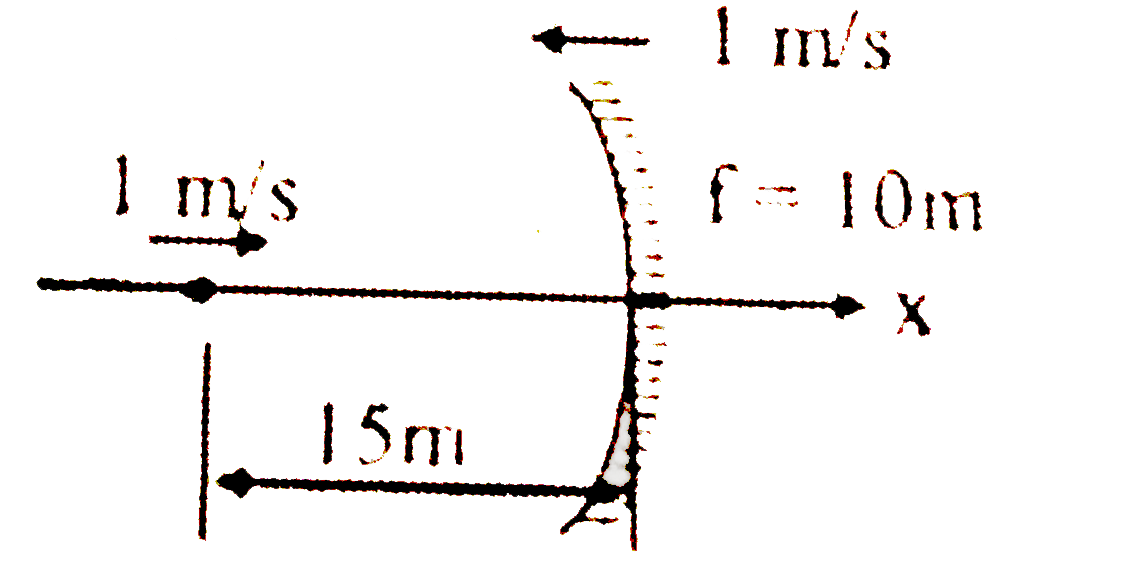 View Solution
View SolutionAn object moves 10 m in 4 s then turns left and moves 20 m in next 5 s. What is the average speed of the object?
View SolutionAn electron moves along a circular path of radius 10 cm. If the centripetal acceleration is 4×1011m/s2 , then its linear speed is
View SolutionAn object is moving in x−y plane its velocity and acceleration at t=0 are represented in figure.

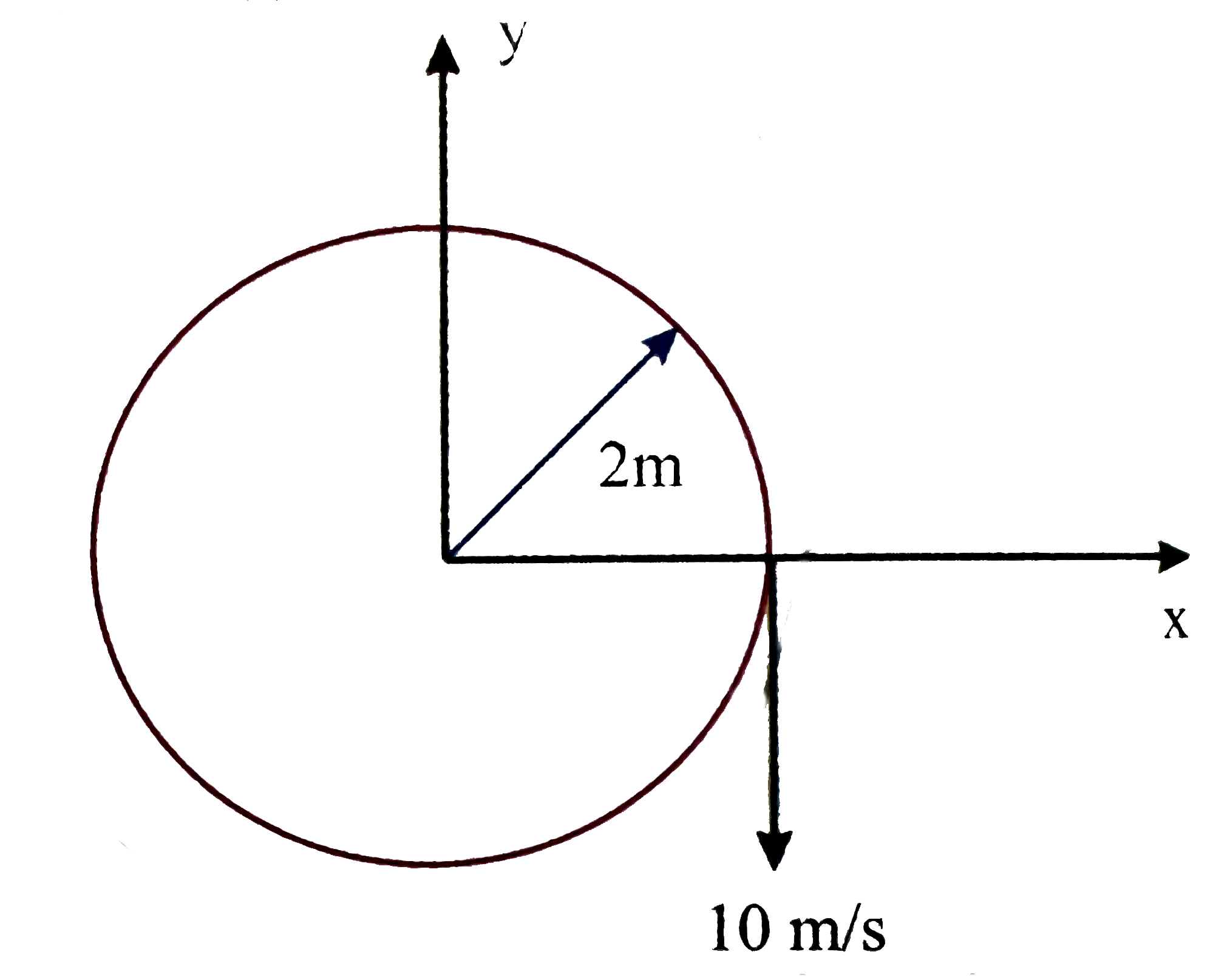
After how much time object crosses the y−axis:-View SolutionA particle is moving along a circular path in xy-plane.When its crosses x-axis,it has an acceleration along the path of 1.5m/s2, and is moving with a speed of 10m/s in −ve y-direction.The total acceleration is
 View Solution
View Solution

