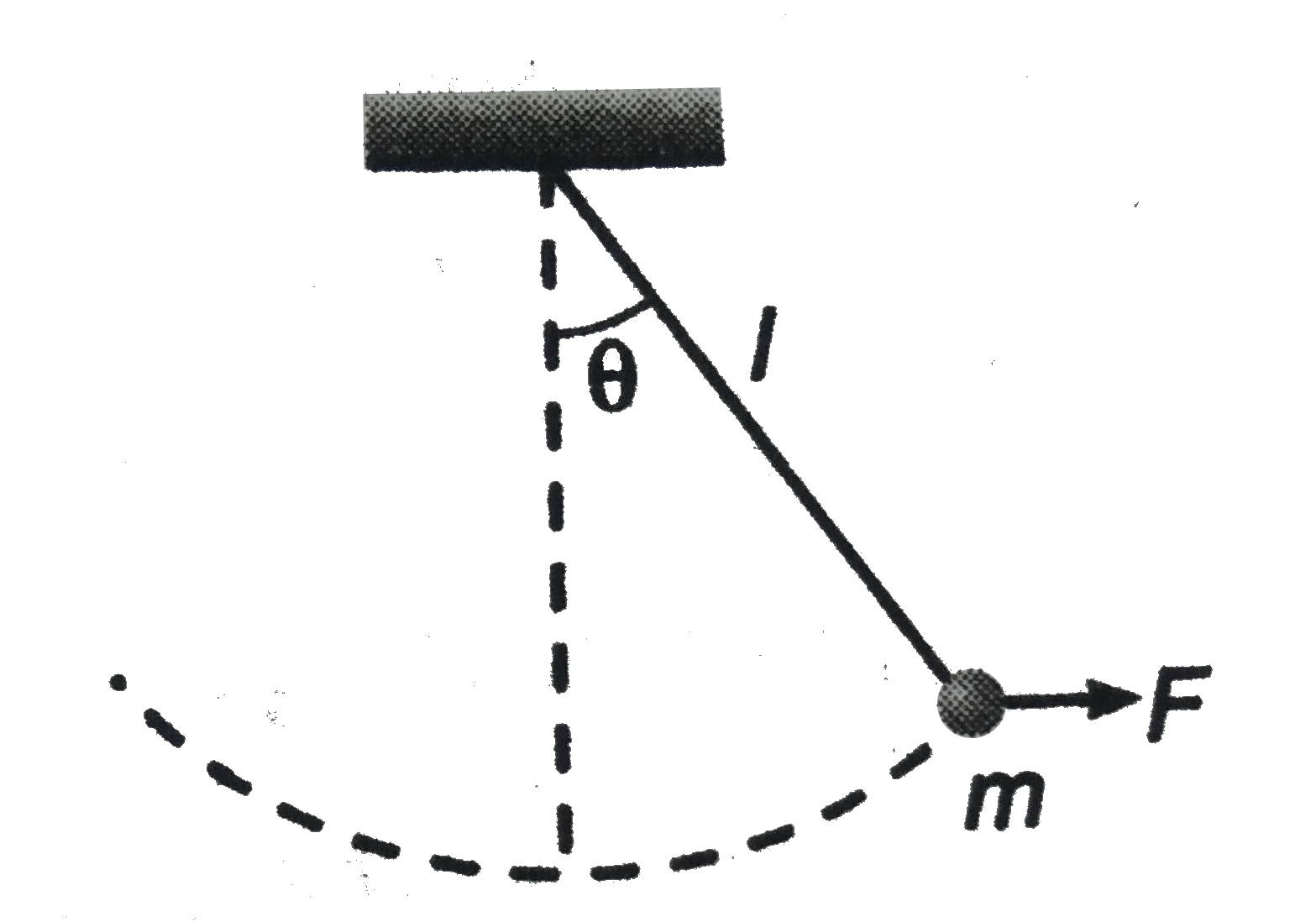
An object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
 .
.
mgl(1+cosθ)
mgl(1−cosθ)
mgl(1−cosθ)
mgl(1+cosθ)
The correct Answer is:C
In this case, three forces are acting on the object:
1. tension (T)
2. weight (mg) and
3. applied force (F)
Using work-enegy theorem
(##DCP_V01_C09_S01_010_S01##).
Wnet=ΔKE
or WT+Wmg+WF=0 ...(i)
as ΔKE=0
because Ki=Kf=0
Further, WT=0, . as tension is always perpendicular to displacement.
Wmg=−mgh
or wmg=−mgl(1−cosθ)
Substituting these values in Eq. (i), we get
WF=mgl(1−cosθ).
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Solved Examples
12 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions

A ball of mass 200g is attached to a string of length 50cm and a force F is applied on it as shown. Find the work done by this force if string makes an angle 60∘ with vertical. In the initial and final position, speed of the ball is zero.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View Solution
Knowledge Check
An object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
 . Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
. Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)A stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
ARadially outwardBRadialy inwardCTangentially outwardDWith acceleration mv2lAn object of mass M is tied to a string of l and revolve in a horizontal circle .If length is reduced by l/2, then period is
AT/√2B2√2TCT/4D2T
A tangential force F is applied on a disc of radius R, due to which it deflects through an angle θ from its initial position. The work done by this force would be
View SolutionA simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
View SolutionA stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View SolutionA force F is applied on a lawn move at an angle of 60∘ with the horizontal. If it moves through a distance x, the work done by the force is
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View Solution
