An observer moves with velocity v1=12c along a straight line. In front of him a source of monochromatic light moves with velocity v2=34c in the same direction and along the same straight line. The proper frequency of light is equal to ω0. Find teh frequency of light registered by the observer.
We go to the frame in which the observer is at rest. In this frame the velocity of the source of light is, by relativistic velocity addition formula,
v=34c−12c1−(34c.12c/c2)=2c5
When this source emits light of proper frequency ω0, the frequency recorded by observer will be
ω=ω0√1−v/c1+v/c+v/c=√37ω0
Note that ω<ω0 as the sourcee is moving away form the observer (red shift).
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation
47 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionA source of light moves with velocity v relative to a receiver. Demonstrate that for v<<c the fractional variation of frequency of light is defined by Eq.
View Solution
Knowledge Check
A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
Av2−v1t1−t2Bv2−v1t1+t2Cv2−t1t2−t1Dv1+v2t1−t2If the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
AasBsCs2D2sIf source and observer are moving towards each other with a velocity vradial anf c indicates velocity of light, then, fractional change in frequency of light due to Doppler's effect will be
AΔvv=vradialcBΔvv=−vradialcCΔvv=cvradialDΔvv=−cvradial
A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is
View SolutionA particle moves in a straight line from A to B with speed v1 and then from B to A with speed v2. Find the average velocity and average speed.
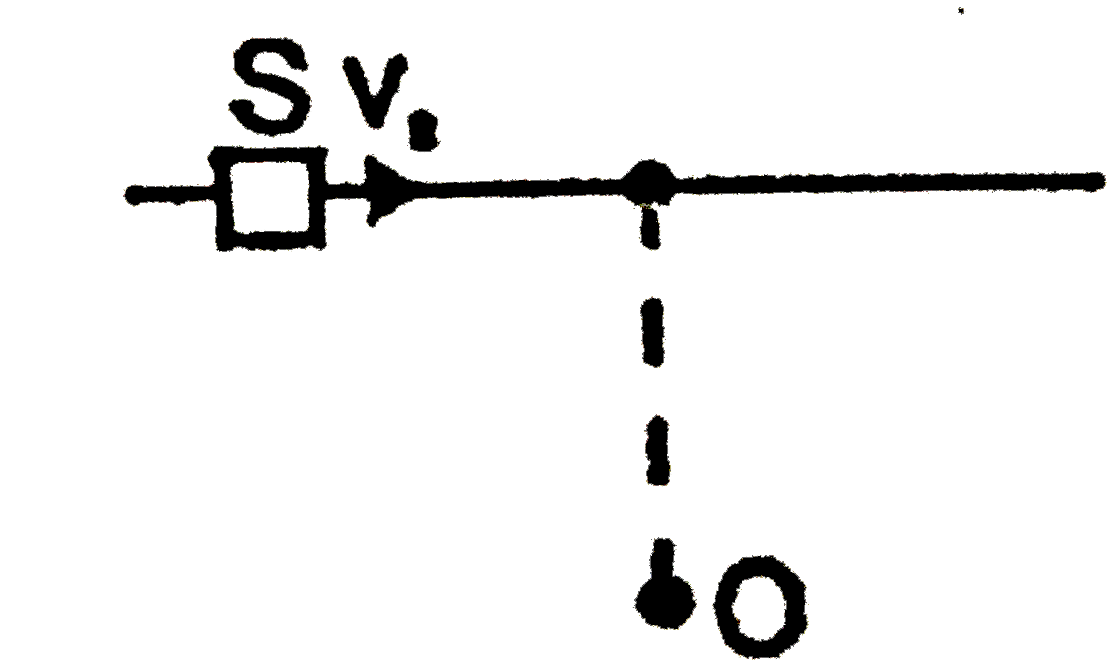
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
View SolutionIf a particle is moving the velocity v(t)=cos πt, along a straight line such that at t=0, s=4, its position function is given by
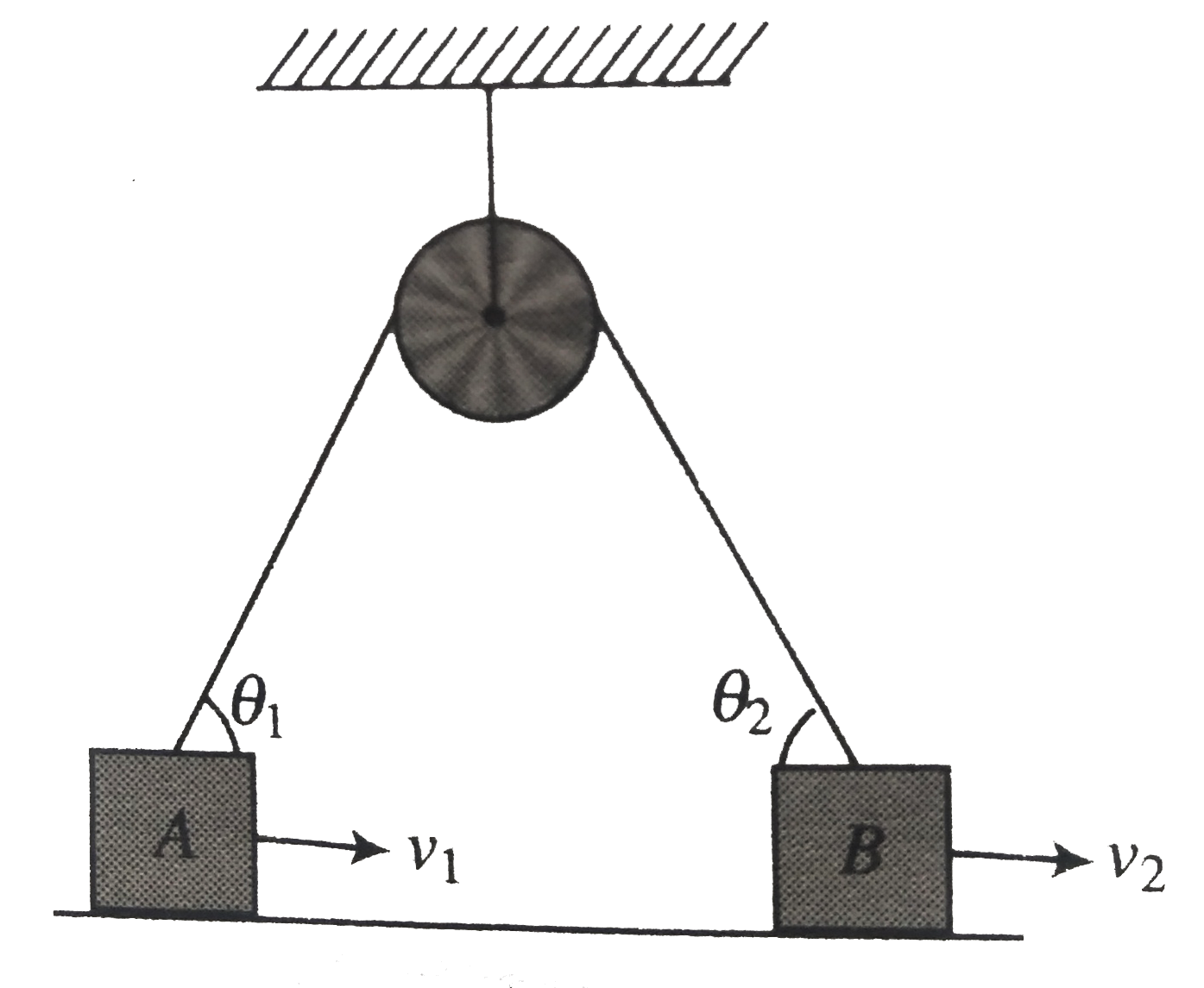
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
View Solution
