An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
Here, initially, of tube extends above the mercury level.
.
= atmospheric pressure
When tube is raised further by 0.43 m
let h be the length of air column above the mercury level. ltbr>
and
As
.
Topper's Solved these Questions
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - NCERT questions
13 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Higher order thinking skills questions
9 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Long answer questions
13 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
Similar Questions
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)
View Solution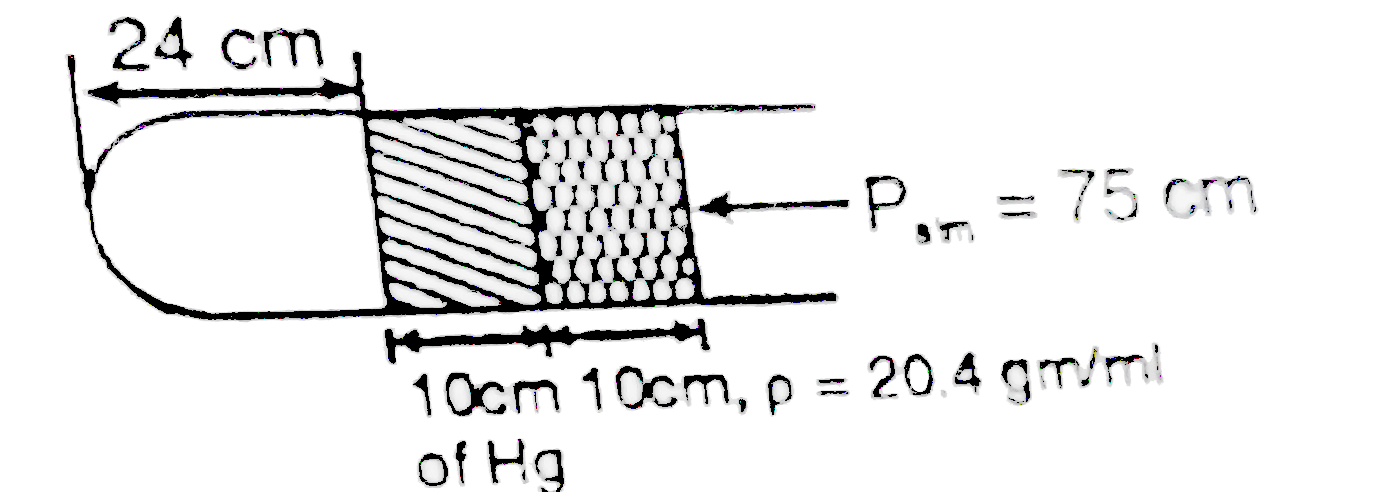
If above tube is placed vertically with the open and upward then find the length of the air column.
View Solution
Knowledge Check
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)A38 cmB6 cmC16 cmD22 cmAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. what will be length of the air column above mercury in the above now ?
(Atmospheric pressure = 76 cm of Hg)A38 cmB6 cmC16 cmD22 cmA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
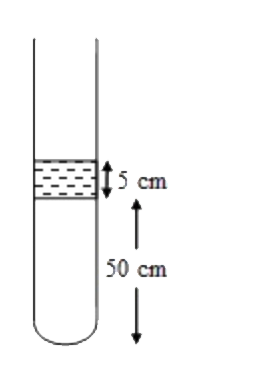 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cm
An open glass tube is immersed in mercury so that a length of 8cm of the tube projects above the mercury. The tube is then closed and raised through 44cm. What length of the tube will be occupied by the air after it has been raised? Given 1 atm =76cm of Hg.
View Solution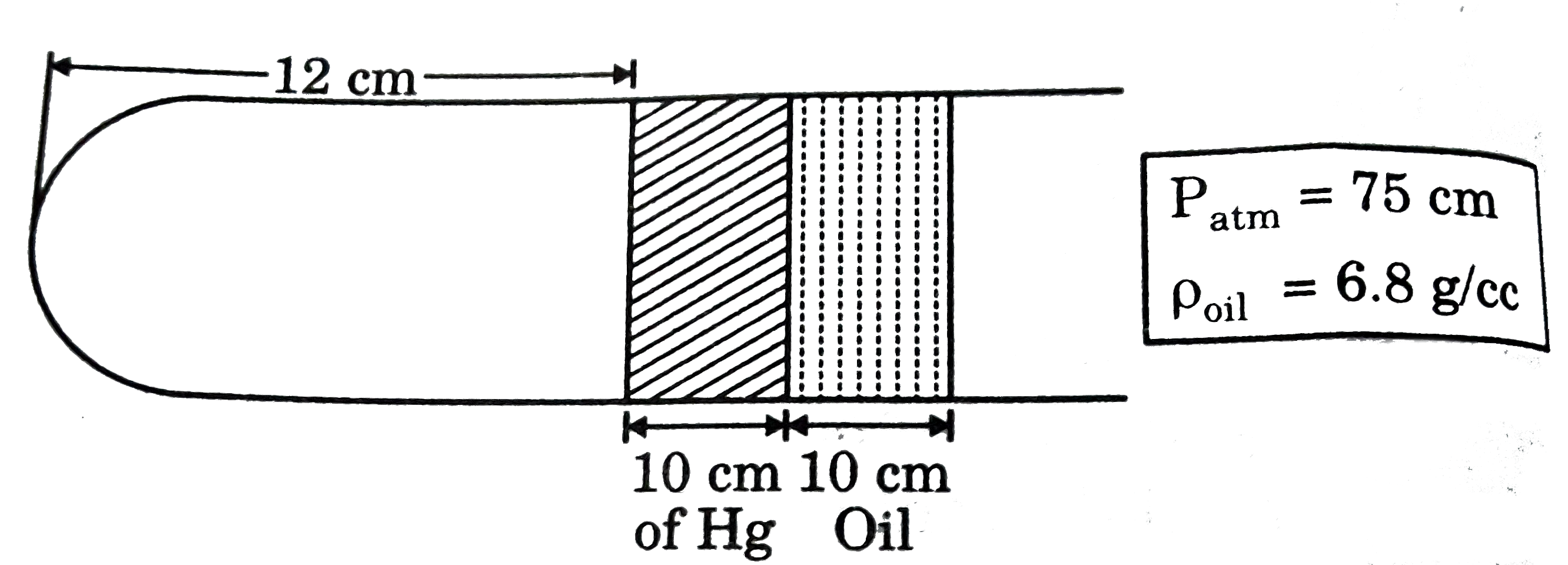
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionA quill tube contains a mercury column of length 19cm. The length of air column is 24cm when it is held veritcally. On inverting it with its open end downwards the length of air column will be
(atmospheric pressure =76cm of Hg)
View SolutionSome mercury is poured into a capillary tube of uniform bore and one end closed. When the tube is held horizontally, mercury column has a length of 4 cm and air enclosed in the closed end has a length of 10 cm. If the tube is now held vertically, with open end upwards, the length of the air column will be (take atmospheric pressure at the place of experiment to be 760 mm)
View Solution
