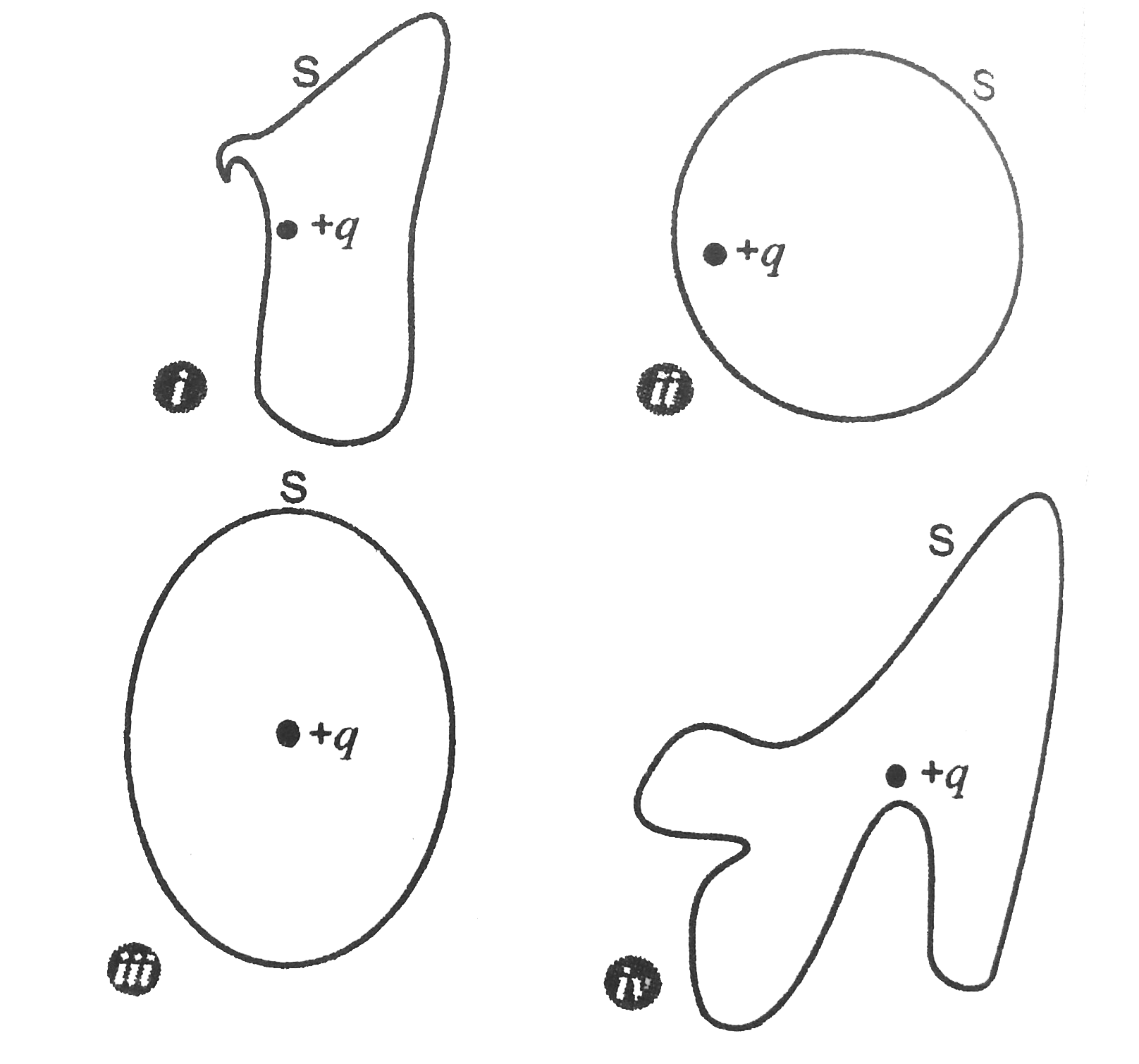
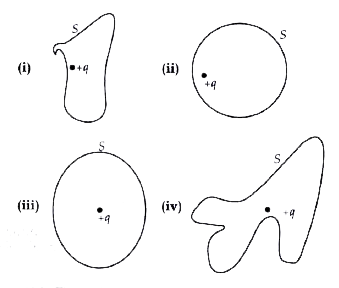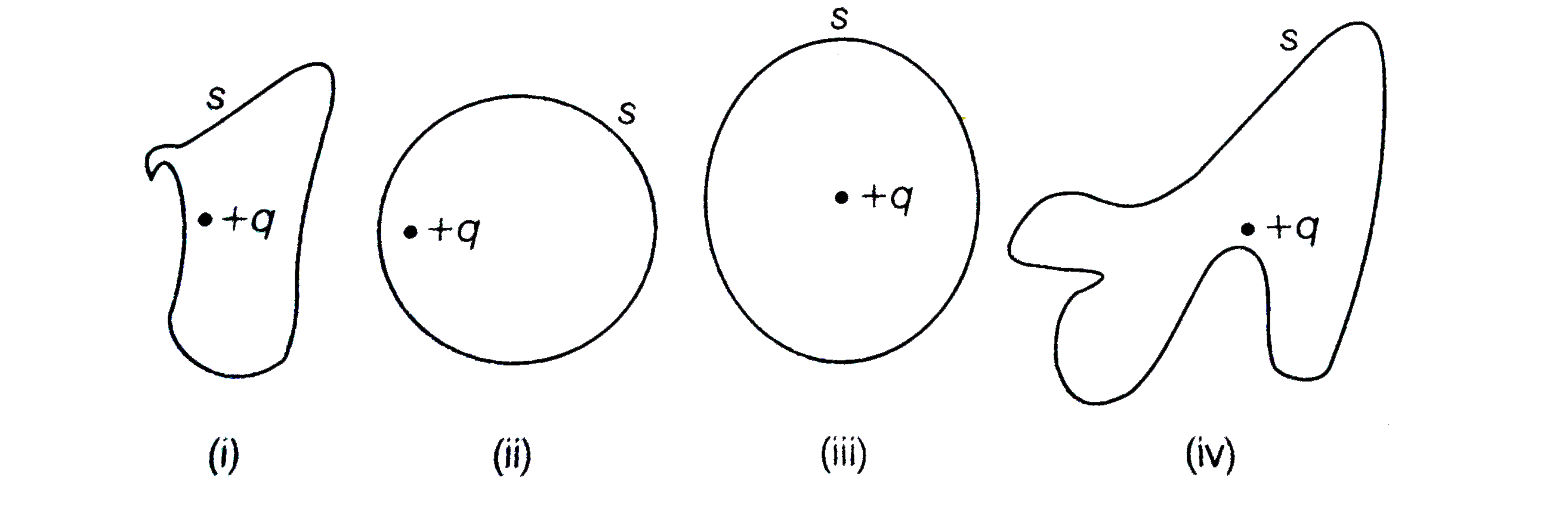Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
Consider a closed surface having certain charges both within and outside as shown. The total electric flux of the given closed surface is : (##U_LIK_SP_PHY_XII_C01_E03_011_Q01.png" width="80%">
A
+2.26×105Vm
B
+7.91×105Vm
C
−2.26×105Vm
D
+1.36×10−6Vm
Text Solution
The correct Answer is:c
ϕE=1∈0∑qen=−2μC8.85×10−12=)−2×10−68.85×10−12=−2.26×105Vm]
|
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - MULTIPLE CHOICE QUESTIONS
30 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - FILL IN THE BLANKS
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ADDITIONAL EXERCISES
10 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Video
Similar Questions
Knowledge Check
Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
What is the electrical flux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?Aq∈0B2q∈0Cq8∈0Dq∈0.6a2Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.Abe doubledBincreases four timesCbe reduced to half.Dremain the same.Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A square surface of side L m is in the plane of paper. A uniform electric field →EVm−1 , also in the plane of the paper, is limited only to the lower half of the square surface as shown in adjoining figure. The electric flux, in SI units, associated with the surfer is :
(##U_LIK_SP_PHY_XII_C01_E03_012_Q01.png" width="80%">AzeroBEL2CEL22∈0DEL22