Are the magnitude and direction fo (→A−→B) .
same as that of (→A−→B) ?
To determine whether the magnitude and direction of →A−→B are the same as that of →B−→A, we will analyze both vectors step by step.
Step 1: Define the Vectors
Let:
- →A=Ax^i+Ay^j+Az^k
- →B=Bx^i+By^j+Bz^k
Step 2: Calculate →A−→B
The vector subtraction →A−→B can be computed as:
→A−→B=(Ax−Bx)^i+(Ay−By)^j+(Az−Bz)^k
Step 3: Calculate →B−→A
Similarly, the vector subtraction →B−→A is given by:
→B−→A=(Bx−Ax)^i+(By−Ay)^j+(Bz−Az)^k
This can be rewritten as:
→B−→A=−(→A−→B)
Step 4: Determine the Magnitudes
The magnitude of →A−→B is:
|→A−→B|=√(Ax−Bx)2+(Ay−By)2+(Az−Bz)2
The magnitude of →B−→A is:
|→B−→A|=√(Bx−Ax)2+(By−Ay)2+(Bz−Az)2
Since (Bx−Ax)=−(Ax−Bx), we can see that:
|→B−→A|=√(−(Ax−Bx))2+(−(Ay−By))2+(−(Az−Bz))2=|→A−→B|
Thus, the magnitudes are equal:
|→A−→B|=|→B−→A|
Step 5: Determine the Directions
The direction of →A−→B is given by the unit vector:
^dA−B=→A−→B|→A−→B|
The direction of →B−→A is:
^dB−A=→B−→A|→B−→A|=−(→A−→B)|→A−→B|=−^dA−B
This shows that the directions are opposite.
Conclusion
The magnitudes of →A−→B and →B−→A are the same, but their directions are opposite.
Final Answer
The magnitude of (→A−→B) is the same as that of (→B−→A), but their directions are opposite.
---
Let:
- →A=Ax^i+Ay^j+Az^k
- →B=Bx^i+By^j+Bz^k
The vector subtraction →A−→B can be computed as:
→A−→B=(Ax−Bx)^i+(Ay−By)^j+(Az−Bz)^k
Similarly, the vector subtraction →B−→A is given by:
→B−→A=(Bx−Ax)^i+(By−Ay)^j+(Bz−Az)^k
This can be rewritten as:
→B−→A=−(→A−→B)
The magnitude of →A−→B is:
|→A−→B|=√(Ax−Bx)2+(Ay−By)2+(Az−Bz)2
|→B−→A|=√(Bx−Ax)2+(By−Ay)2+(Bz−Az)2
Since (Bx−Ax)=−(Ax−Bx), we can see that:
|→B−→A|=√(−(Ax−Bx))2+(−(Ay−By))2+(−(Az−Bz))2=|→A−→B|
Thus, the magnitudes are equal:
|→A−→B|=|→B−→A|
The direction of →A−→B is given by the unit vector:
^dA−B=→A−→B|→A−→B|
^dB−A=→B−→A|→B−→A|=−(→A−→B)|→A−→B|=−^dA−B
This shows that the directions are opposite.
The magnitudes of →A−→B and →B−→A are the same, but their directions are opposite.
The magnitude of (→A−→B) is the same as that of (→B−→A), but their directions are opposite.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Very short
24 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 5 Very short
5 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Very short
22 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
Knowledge Check
Two vectors →A and →B have equal magnitudes. If magnitude of →A−→B is equal to (n) times the magnitude of →A−→B, then angle between →A and →B is ?
Acos−1(n−1n−1)Bcos−1(n2−1n2+1)Ccos−1(n−1n−1)Dcos−1(n2−1n2+1)The resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
A30∘B45∘C150∘D120∘Two vector →Vand→V have equal magnitudes. If magnitude of →A+→B is equal to n time the magnitude of →A−→B, then angel to between →Aand→B is
Acos−1(n−1n+1)Bcos−1(n2−1n2+1)Csin−1(n−1n+1)Dsin−1(n2−1n2+1)
Two vectors →Aand→B have equal magnitudes.If magnitude of (→A+→B) is equal to n times of the magnitude of (→A−→B) then the angle between →Aand→B is :-
View SolutionGive →A+→B+→C+→D =0,whichofthefollow∈gstatementsarecorrect?<br>(a) vec A, vec B ,vec C abd vec Cμsteachbeaνll→−−→r.<br>(b)Themagnitudeof ( vec A + vec C)equalsthemagnitudeof ( vec B + vec D0.<Br>(c)Themagnitudeof vec Acan≠verbegreaterthanthe∑ofthemagnitudeof vec B , vec C and→D.
( d) →B+→C must lie in the plance of →A+→D.if→Aand→D are not colliner and in the line of →A and →D, if they are collinear.
View SolutionTwo vectors →A and →B have precisely equal magnitudes. For the magnitude of →A+→B to be larger than the magnitude of →A−→B by a factor of n, what must be the angle between them?
View SolutionThe three vectors →A,→Band→C are repesented in magnitude and direction by −−−−−−−→OP,−−→OQ, show that (S) is the mid point of (PQ).
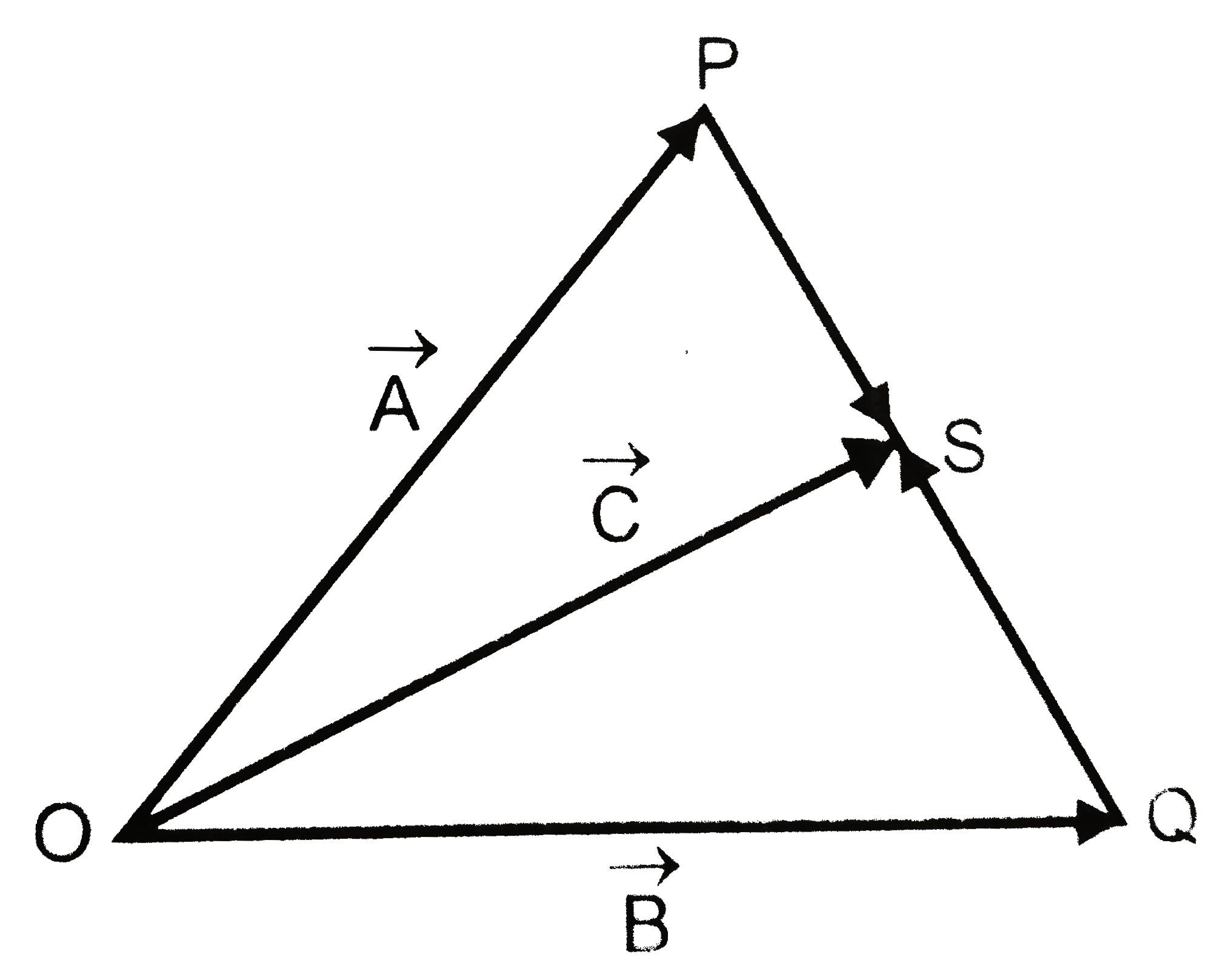 .
.
View SolutionTwo vectors →A&→B have the same magnitude. Under what circumstances does the vector →A+→B have the same magnitude as ∣∣→A∣∣or∣∣→B∣∣. When does the vector difference →A−→B have this magnitude.
View Solution
