AS heavy uniform rod is hanging verticallly from a fixed support. It is streetched by its own weight. The diameter of the rod is
smallest at the top and graduay increases down the rod
largest at the top and gradually decreases down the rod
uniform everywhere
maximum iln the middle
Step by step video & image solution for AS heavy uniform rod is hanging verticallly from a fixed support. It is streetched by its own weight. The diameter of the rod is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 2
7 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
A heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View SolutionA uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
View Solution
Knowledge Check
A unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmA horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
AWBW2C3W4DW4A uniform one metre long rod AB of weight 17 kg is suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively. The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking. Then the position where a weight of 2 kg can be attached to the rod without breaking either of the strings is
A10 cm from AB12 cm from AC13 cm from ADNone of these
A uniform heavy rod of weight 10 kg ms−2, cross-sectional area 100 cm2 and length 20 cm is hanging from a fixed support. Young modulus of the material of the rod is 2×1011Nm−2 Neglecting the lateral contraction, find the elongation of rod due to its own weight:
View SolutionA wire ring of radius R is fixed in a horizontal plane. The wire of the ring has a resistance of λΩm–1. There is a uniform vertical magnetic field B in entire space. A perfectly conducting rod (l) is kept along the diameter of the ring. The rod is made to move with a constant acceleration a in a direction perpendicular to its own length. Find the current through the rod at the instant it has travelled through a distance x=R2.
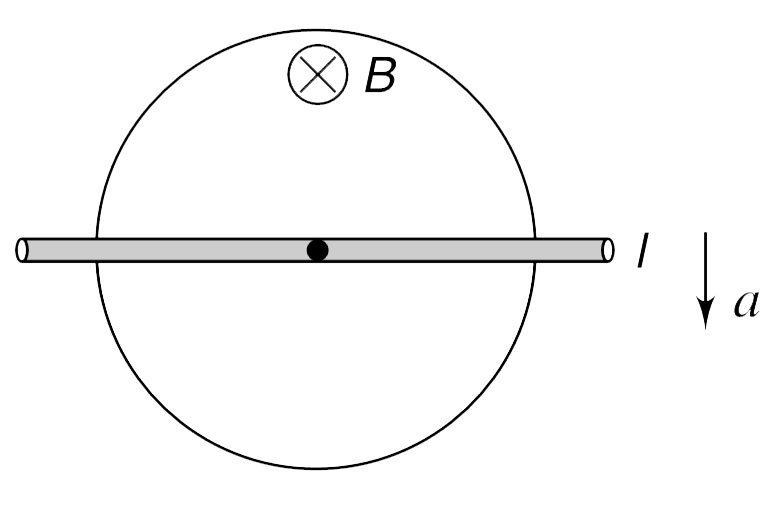
View SolutionA uniform one metre long rod AB of 17 kg weight I suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively .The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking .Find where a weight of 2 kg can be attached to the rod without breaking either of the string .
View SolutionA uniform rod of length l is held vertically on a horizontal floor fixing its lower end, the rod is allowed to fall onto the ground. Find (i) its angular velocity at that instant of reaching the ground (ii) The linear velocity with which the tip of rod hits the floor.
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .
.
View Solution
