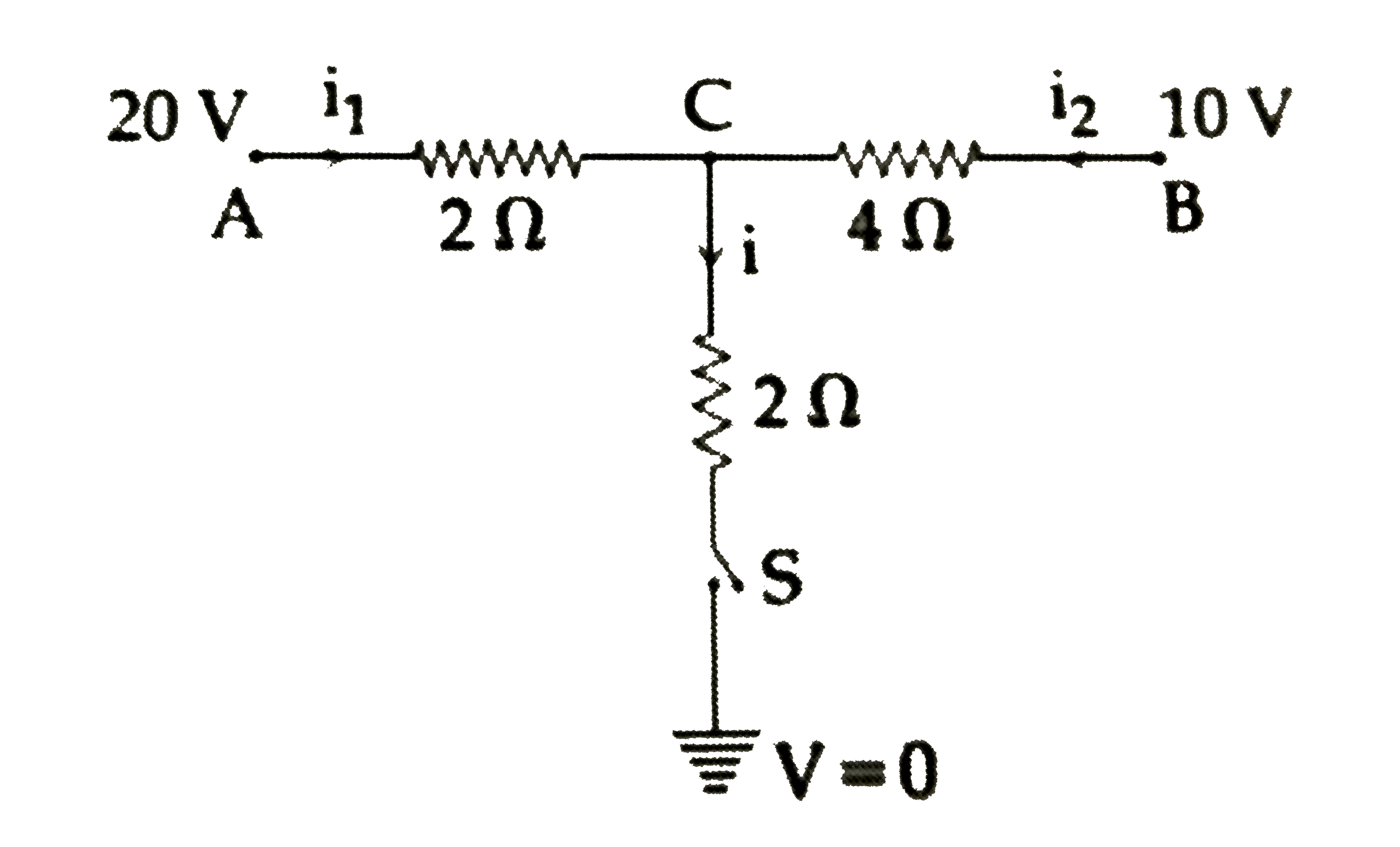
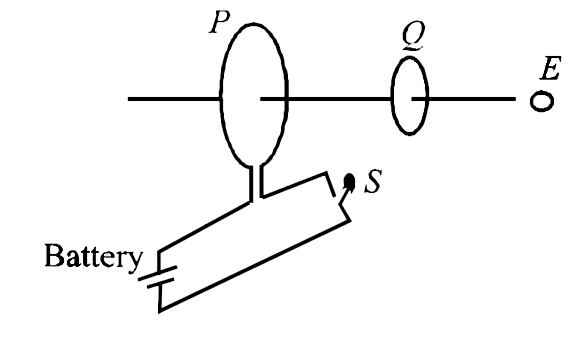
As shown in the figure, P and Q are two coaxial conducting loops separated by some distance. When the switch S is closed, a clockwise current IP (as seen by E) and an induced current IQ1 flows in Q. The switch remains closed for a long time. when S is opened, a current IQ2 flows in Q. Then the direction IQ1andIQ2 (as seen by E) are
A
Respectively clockwise and anticlockwise
B
both clockwise
C
both anticlockwise
D
respectively anticlockwise and clockwise
Video Solution
Text Solution
The correct Answer is:D
When swich S is closed magnetic field lined passing through Q increases in the direction from right to left. So, according to Lenz's law induced current in Q i.e., IQ1 will flow in such a direction so that the magnetic field lines due to IQ2 passes from left to right through Q. this is possible when IQ1 flows in anticlockwise direction as seen by E. Opposite is the case when switch S is opened i.e., IQ2 will be clockwise as seen by E
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Motional And Rotational Emf
95 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Inductor Circuits
31 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
In fig. A2.27, the charge that flows from P to Q when the switch S is closed is
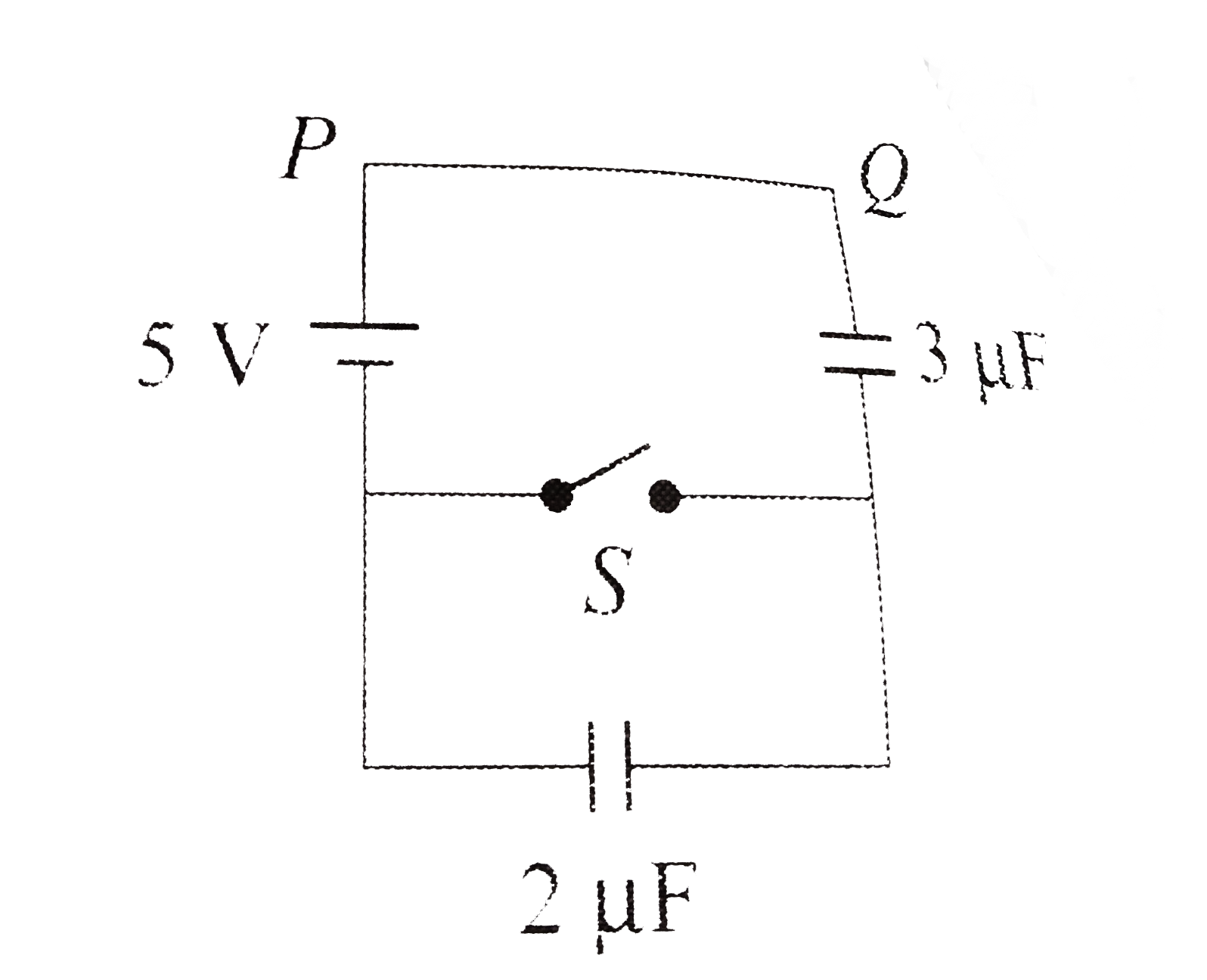 A3μCB6μCC9μCD15μC
A3μCB6μCC9μCD15μCIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
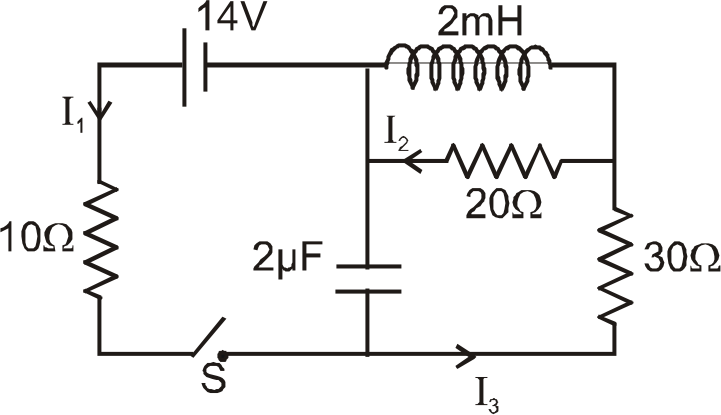 A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6A
A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6AIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are
 Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
Consider the circuit shown in figure. Find the current through the 10Ω resistor when the switch S is (a) opened (b) closed.
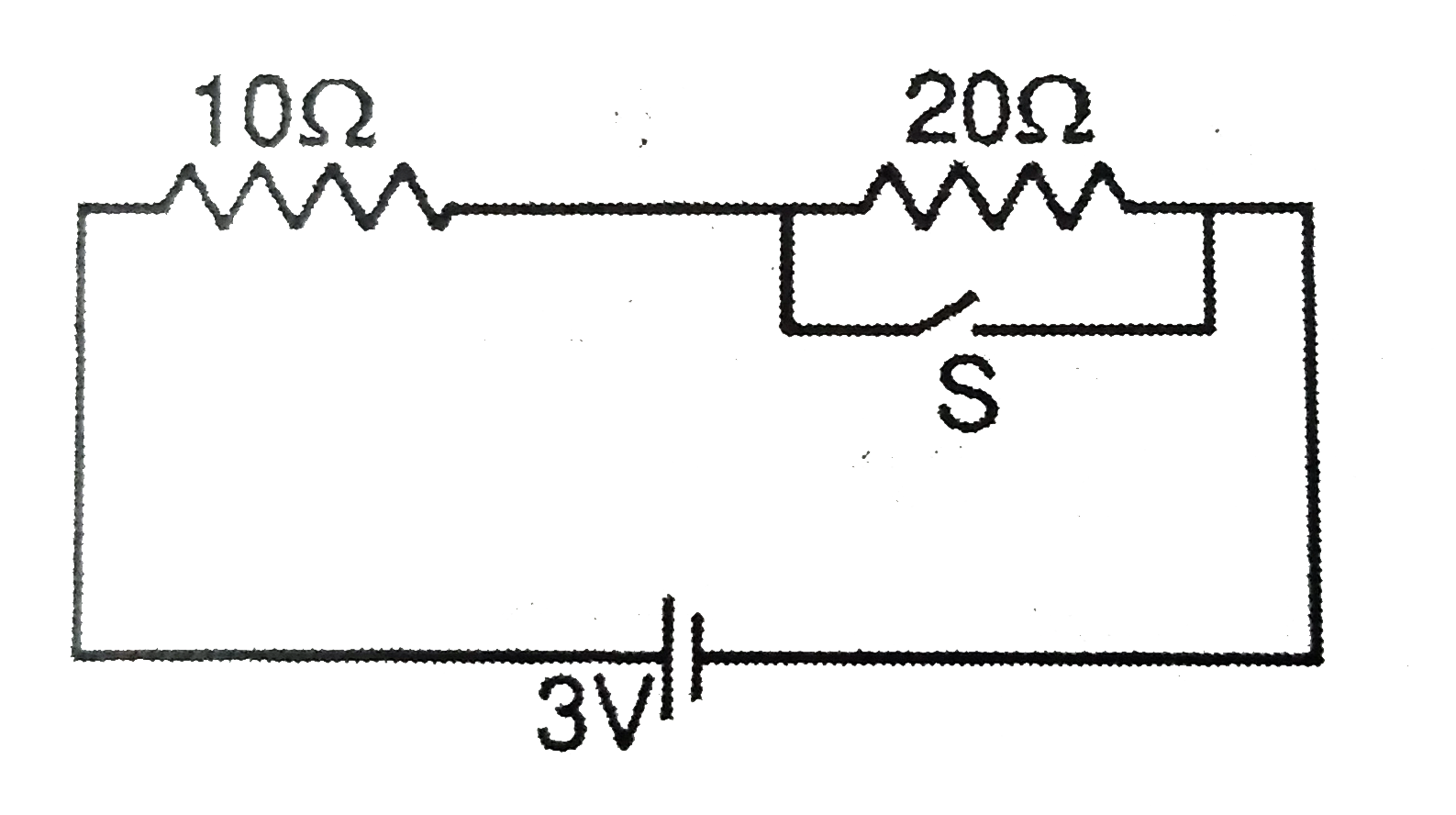
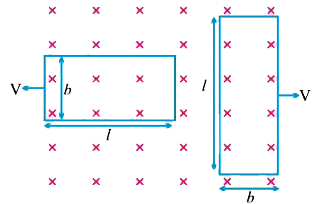
View SolutionIn the figure shown, coils P and Q are identical and moving apart with same velocity V. Induced currents in the coils are I1andI2. Find I1/I2.
View SolutionIn the circuit shown in figure switch S is closed at time t=0
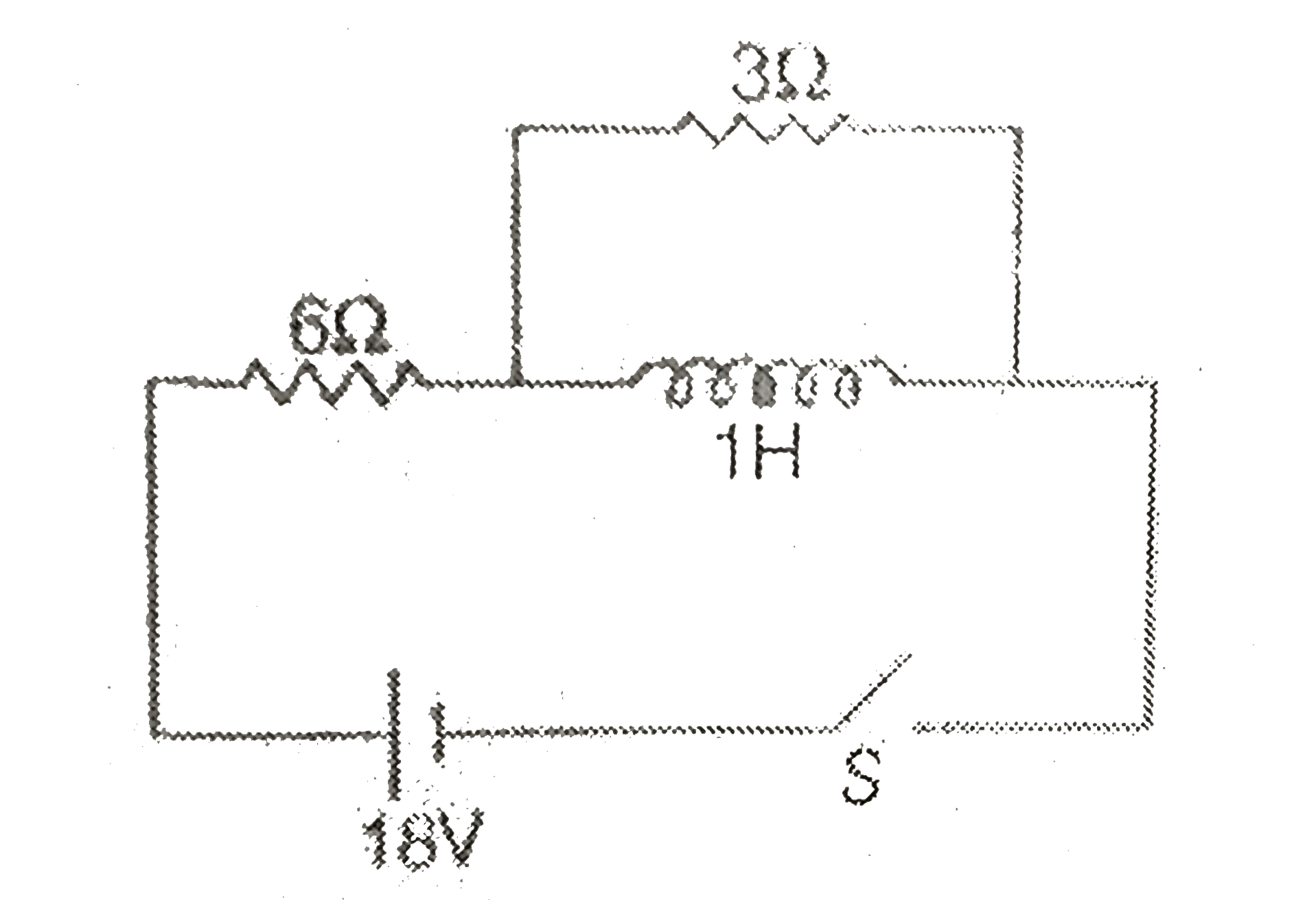
Current I from the battery at time t is given by
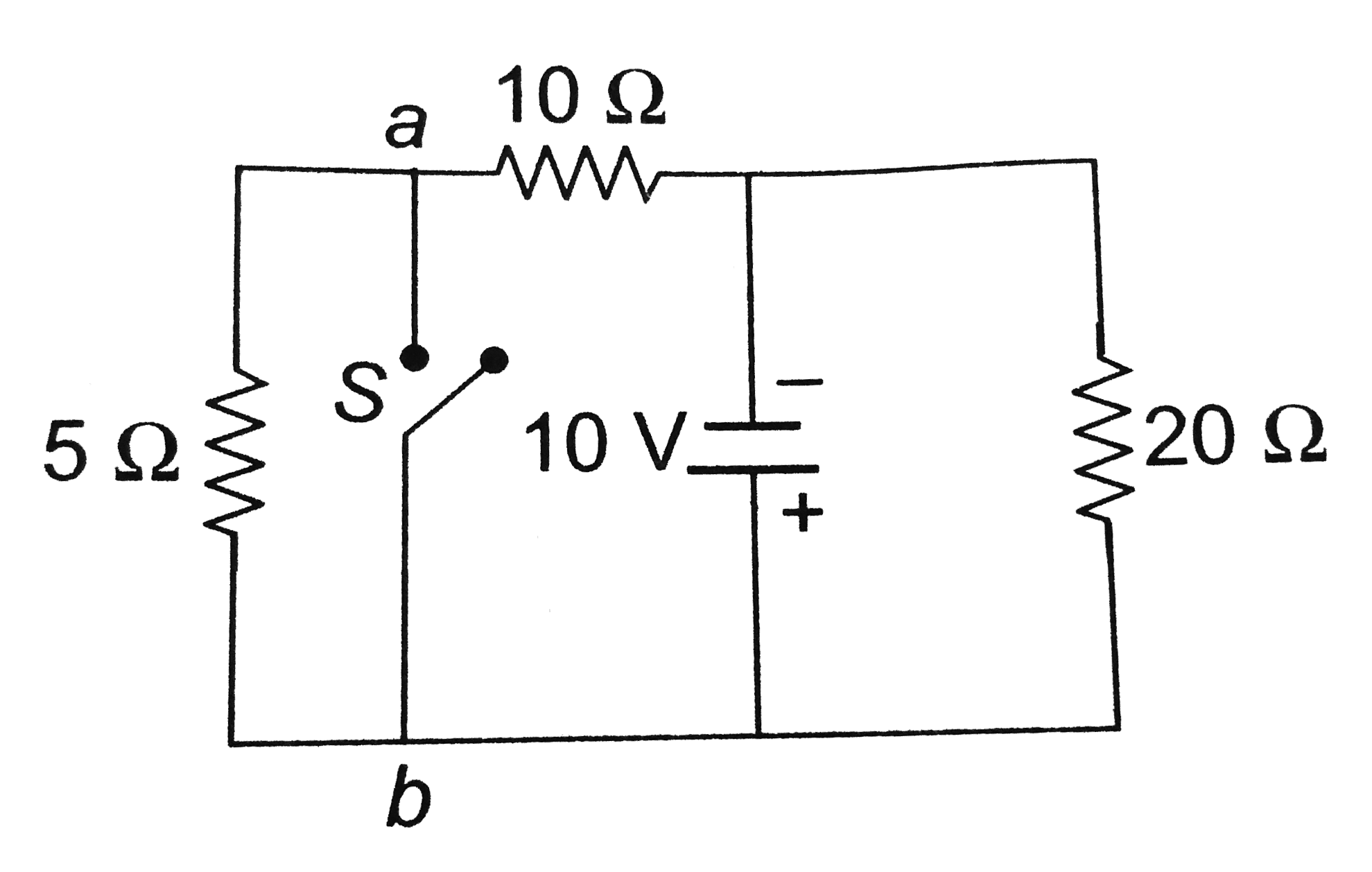
View SolutionIn the circuit shown below, the current that flows from a to b when switch S is closed is
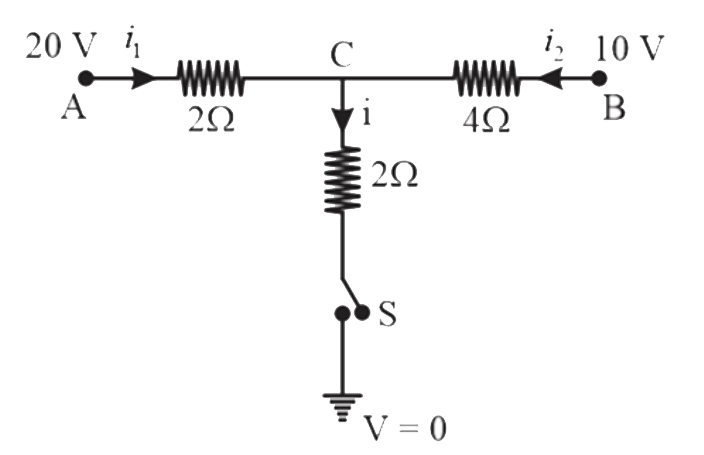
View SolutionWhen the switch S, in the circuit shown , is closed , then the Value of current i will be :
View Solution