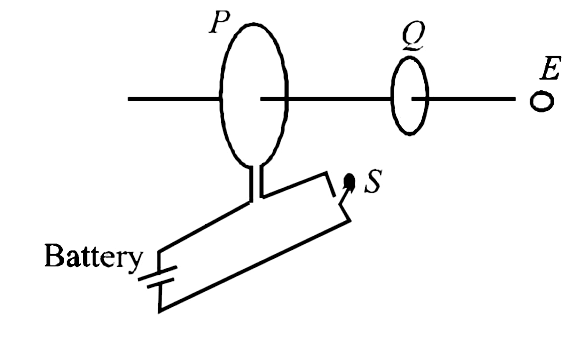
As shown in the figure, P and Q are two coaxial conducting loops separated by some distance. When the switch S is closed, a clockwise current IP (as seen by E) and an induced current IQ1 flows in Q. The switch remains closed for a long time. when S is opened, a current IQ2 flows in Q. Then the direction IQ1andIQ2 (as seen by E) are
A
respectively clockwise and anti-clockwise
B
both clockwise
C
both anti-clockwise
D
respectively anti-clockwise and clockwise
Video Solution
Text Solution
The correct Answer is:D
When switch S is closed magnetic field lines passing through Q increases in the direction from right to left.
So, according to Lenz's law, induced current in Q, i.e., IQ1 will flow in such a direction, so that the magnetic field lines due to IQ1 passes from left to right through Q. This is possible when IQ1 flows in anti-clockwise direction as seen by E. Opposite is the case when switch S is opened, i.e., IQ2 will be clockwise as seen by E.
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
In fig. A2.27, the charge that flows from P to Q when the switch S is closed is
 A3μCB6μCC9μCD15μC
A3μCB6μCC9μCD15μCIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
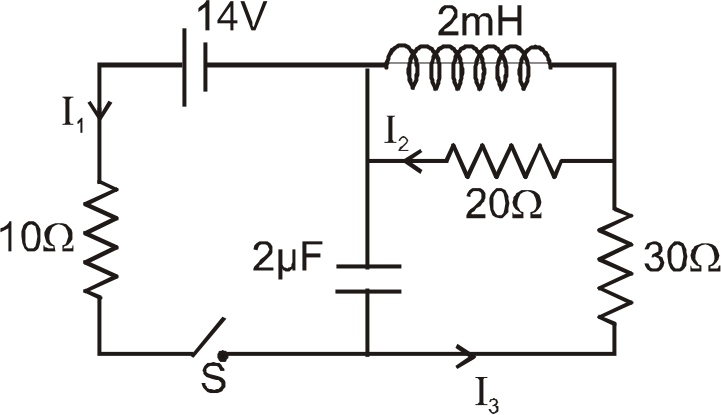 A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6A
A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6AIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are
 Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
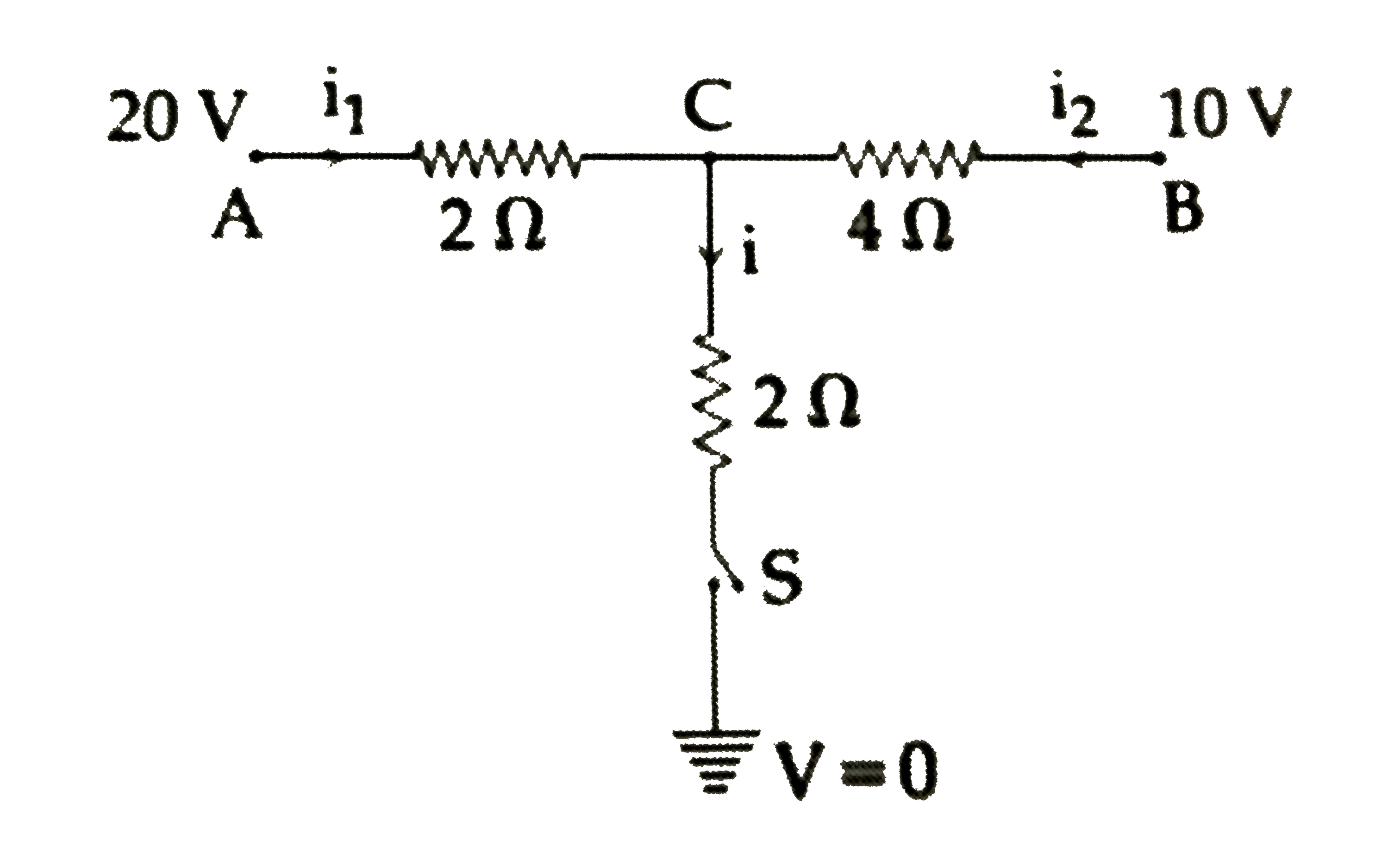
Consider the circuit shown in figure. Find the current through the 10Ω resistor when the switch S is (a) opened (b) closed.

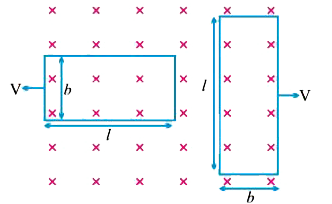
View SolutionIn the figure shown, coils P and Q are identical and moving apart with same velocity V. Induced currents in the coils are I1andI2. Find I1/I2.
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given by
View SolutionIn the circuit shown below, the current that flows from a to b when switch S is closed is

View SolutionWhen the switch S, in the circuit shown , is closed , then the Value of current i will be :
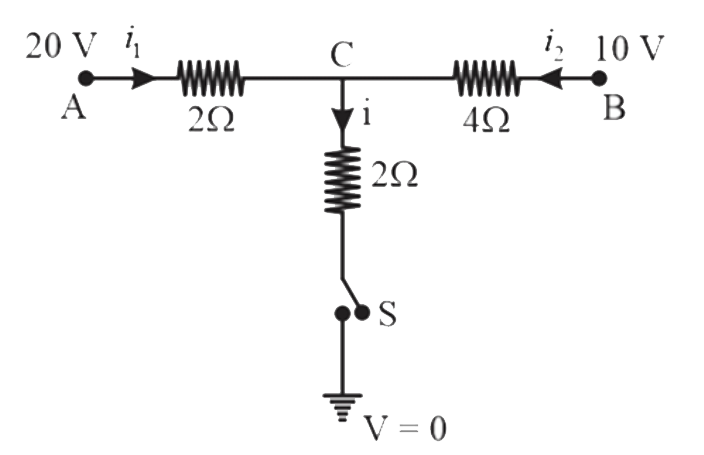
View Solution