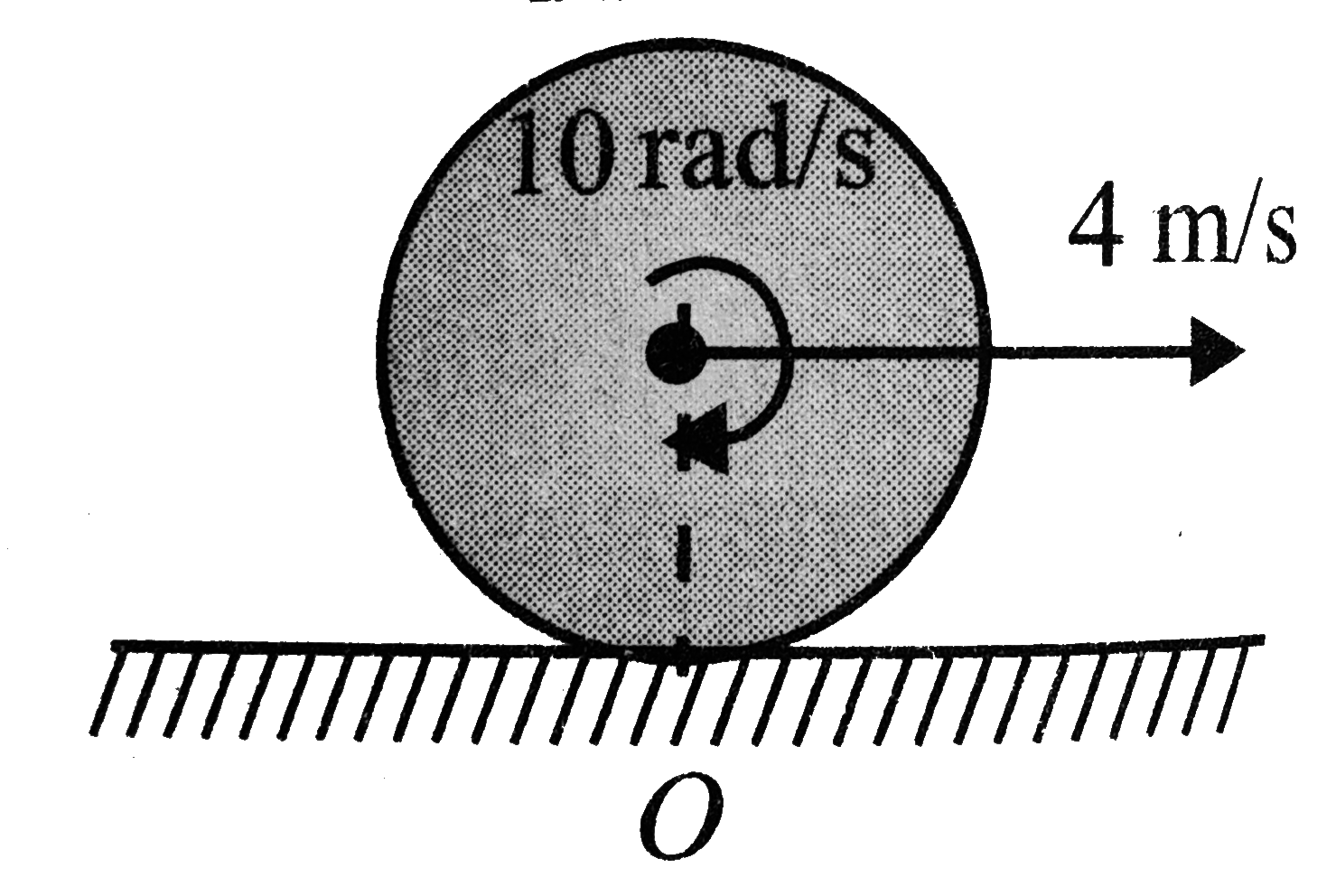
Assertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.
Assertion is True, Reason is True, Reason is a correct explanation for Assertion
Assertion is True, Reason is True, Reason is not a correct explanation for Assertion
Assertion is False but, Reason is True.
Assertion is True, Reason is False
The correct Answer is:A
Step by step video, text & image solution for Assertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v. Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.

View SolutionA circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View Solution
Knowledge Check
A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
AzeroBvC2vD√2vA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)A disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.
 AVB2VC3VD2V3
AVB2VC3VD2V3
A disc of mass 100 g is rolling without slipping on a horizontal surface with a velocity of 10cms−1. Calculate its total energy.
View SolutionA disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
View SolutionA ring and a disc of same mass roll without slipping along a horizontal surface with same velocity. If the K.E. of ring is 8J, then that of disc is
View SolutionA disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
View SolutionA uniform ring rolls on a horizontal surface with out slipping. Its centre of mass moves with a constant speed v. then speed of the upper most point on its rim above the ground is
View Solution
