Assertion : A particle is projected with velocity u at angle 45∘ with ground. Let v be the velocity of particle at time (≠0), then value of u.v can be zero.
Reason : Value of dot product is zero when angle between two vectors is 90∘
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:B
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Understand the Assertion
The assertion states that a particle is projected with velocity u at an angle of 45∘ with the ground. We need to determine if the dot product u⋅v can be zero at some time t≠0.
Step 2: Analyze the Motion
In projectile motion, the velocity of the particle can be broken down into two components:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
At any time t, the velocity v of the particle can be expressed as:
- vx=ux=u√2 (remains constant)
- vy=uy−gt=u√2−gt
Step 3: Determine the Condition for Dot Product to be Zero
The dot product u⋅v is given by:
u⋅v=|u||v|cos(θ)
where θ is the angle between the vectors u and v. For the dot product to be zero, cos(θ) must be zero, which occurs when θ=90∘.
Step 4: Find When θ=90∘
The angle between the initial velocity vector u and the velocity vector v at time t can be determined. As the particle moves, at the peak of its trajectory, the vertical component of the velocity vy becomes zero, and the velocity vector v is purely horizontal. At this point, the angle between u (which has both horizontal and vertical components) and v (which is horizontal) is 90∘.
Step 5: Conclusion on Assertion
Since at the peak of the projectile's motion, the angle between u and v becomes 90∘, the dot product u⋅v can indeed be zero at that moment. Thus, the assertion is true.
Step 6: Analyze the Reason
The reason states that the value of the dot product is zero when the angle between the two vectors is 90∘. This is a true statement regarding the properties of the dot product.
Step 7: Relationship Between Assertion and Reason
While both the assertion and reason are true, the reason does not specifically explain the assertion in the context of projectile motion. The assertion discusses a specific scenario in projectile motion, while the reason discusses a general property of dot products.
Final Answer
Both the assertion and reason are true, but the reason is not the correct explanation of the assertion. Therefore, the correct answer is Option B.
---
The assertion states that a particle is projected with velocity u at an angle of 45∘ with the ground. We need to determine if the dot product u⋅v can be zero at some time t≠0.
In projectile motion, the velocity of the particle can be broken down into two components:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
- vx=ux=u√2 (remains constant)
- vy=uy−gt=u√2−gt
The dot product u⋅v is given by:
u⋅v=|u||v|cos(θ)
where θ is the angle between the vectors u and v. For the dot product to be zero, cos(θ) must be zero, which occurs when θ=90∘.
The angle between the initial velocity vector u and the velocity vector v at time t can be determined. As the particle moves, at the peak of its trajectory, the vertical component of the velocity vy becomes zero, and the velocity vector v is purely horizontal. At this point, the angle between u (which has both horizontal and vertical components) and v (which is horizontal) is 90∘.
Since at the peak of the projectile's motion, the angle between u and v becomes 90∘, the dot product u⋅v can indeed be zero at that moment. Thus, the assertion is true.
The reason states that the value of the dot product is zero when the angle between the two vectors is 90∘. This is a true statement regarding the properties of the dot product.
While both the assertion and reason are true, the reason does not specifically explain the assertion in the context of projectile motion. The assertion discusses a specific scenario in projectile motion, while the reason discusses a general property of dot products.
Both the assertion and reason are true, but the reason is not the correct explanation of the assertion. Therefore, the correct answer is Option B.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct
16 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Subjective
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.3
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
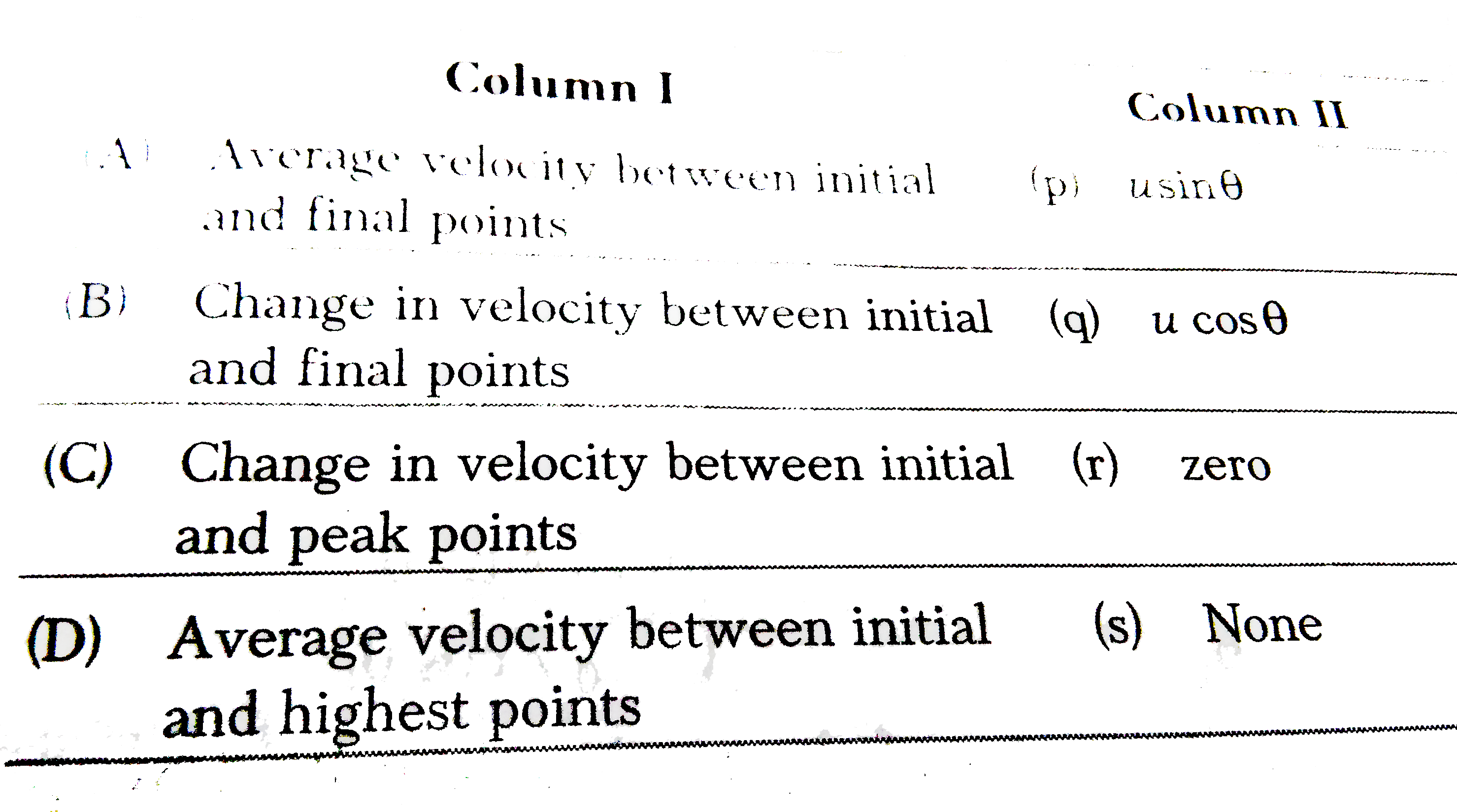
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle of mass m is projected with velocity making an angle of 45∘ with the horizontal When the particle lands on the level ground the magnitude of the change in its momentum will be .
View SolutionA particle is projected with initaial velocity u at an angle 0 with horizontal, then variation of angular momentum L about starting w.r.t. Time t will be
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View Solution
