Assertion : For a simple pendlume the graph between ans T2 is hyperbola
Reason : T=2π√g1
If both assertion and reason are true and the reasopn is correct explanation of the assertion
If both assertion and reason are true and but not the correct explanation of assertion
If assertion is true but the reason is false
If both assertion and reason are false
The correct Answer is:C
From the relation T=2π√1g
or T2=4π2lg
soT2∝1g
Therefore the graph between T2 and g is hyperbola
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - NEET Questions39videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - AIIMS Questions24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Problems Based On Mixed Concepts24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
If the length of a simple pendulum is decreased by 2%, find the percentage decrease in its period T, where T=2π√lg
View SolutionThe time t of a complete oscillation of a simple pendulum of length l is given by the equation T=2π√1g
where g is constant. What is the percentage error in T when l is increased by 1%?View Solution
Knowledge Check
- Question 1 - Select One
The graph between L and T2 is
A B
B C
C D
D
- Question 2 - Select One
The graph between L and T2 is
A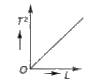 B
B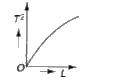 C
C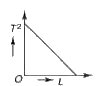 D
D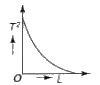
- Question 3 - Select One
For a simple pendulum, the graph between T2andL (where T is the time period & Lis the length) is
Astraight line passing through originBparabolicCcircleDnone of the above
What are the variables in the formula T=2π√lg?
View SolutionWhile determining the value of g using simple pendulum, we plot a graph between l and T2 which is
View SolutionThe graph between the (velocity)2 and temperature T of a gas is
View SolutionAssertion : The length of a simple pendulum is increases by 4% the corresponding decrease in time period will be 2%
Reason : T=∝√1View SolutionAssertion : For a given simple harmonic motion displacement (from the mean position) and acceleration have a constant ratio.
Reason : T=2π√∣∣∣displacementacceleration∣∣∣.View Solution

