Assertion: In y=Asin(ωt−kx),(ωt−kx) is dimensionless.
Reason: Because dimension of ω=[M0L0T].
If both assertion and reason are true and reason is the correct explation of assertion.
If both assertion but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:c
As ω (angular velocity) has the dimension of [T−1] not [T].
Topper's Solved these Questions
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - NEET Questions
23 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - AIIMS Questions
22 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Problems Based On Mixed Concepts
24 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
- VECTORSBOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
In the relation y=rsin(ωt−kx), the dimensions of ω/k are
A[M0L0T0]B[M0L1T−1]C[M0L0T1]D[M0L1T0]if y=Asin(ωt−kx), then the value of dydx is
AAcos(ωt−kx)B−Aωcos(ωt−kx)CAKcos(ωt−kx)D−AKcos(ωt−kx)
(a) the displacement of a particle is given by s−asin(ωt=kx), where t is in second and x is in meter. Find the dimensions of ω and k.
(b) The velocity of a praticle is given by v=v0e−λt, where t is time. Find the dimensions of v0 and λ.
View SolutionIn the expression y=asin(ωt+θ), y is the displacement and t is the time . Write the dimension ofa,ωand θ .
View SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
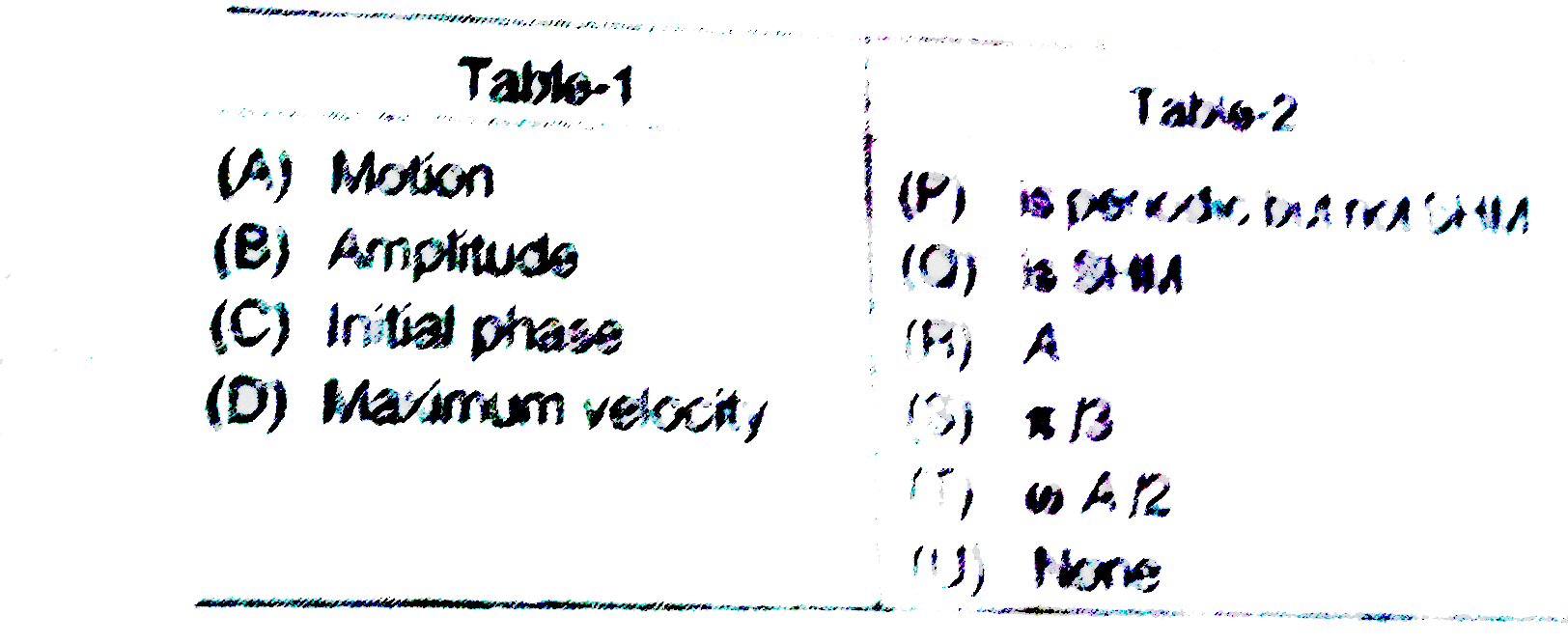
View SolutionIn the equation y= a sin (ωt+kx) t and x stand for time and distance respectively. What are the dimensions of ω/k?
View SolutionIn the relation x=cos(ωt+kx), the dimension(s) of ω is/are
View SolutionIn the equation y=Asin(ωt−kx), obtain the dimensional formula of ωandk. Given x is distnace and t is time.
View Solution
