Assertion : The focal length of an equiconvex lens placed in air is equal to radius of curvature of either face.
Reason : For an equiconvex lens radius of curvature of both the faces is same.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true and reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:B
To solve the problem, we need to analyze the assertion and the reason provided in the question.
Step 1: Understand the Assertion
The assertion states that the focal length (f) of an equiconvex lens placed in air is equal to the radius of curvature (R) of either face of the lens.
Step 2: Understand the Reason
The reason states that for an equiconvex lens, the radius of curvature of both faces is the same. This is indeed true, as an equiconvex lens has two convex surfaces with equal radii of curvature.
Step 3: Use the Lensmaker's Formula
The lensmaker's formula is given by:
1f=(μ−1)(1R1−1R2)
where:
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
For an equiconvex lens:
- Let R1=R (for the first surface),
- Let R2=−R (for the second surface, as per the sign convention).
Step 4: Substitute Values into the Formula
Substituting these values into the lensmaker's formula:
1f=(μ−1)(1R−(−1R))
1f=(μ−1)(1R+1R)
1f=(μ−1)(2R)
Step 5: Substitute the Refractive Index
Assuming the refractive index μ=1.5:
1f=(1.5−1)(2R)
1f=0.5(2R)
1f=1R
Step 6: Solve for Focal Length
Taking the reciprocal gives:
f=R
This confirms that the focal length of the equiconvex lens is indeed equal to the radius of curvature of either face.
Conclusion
Thus, both the assertion and the reason are true, but the reason does not correctly explain the assertion. The correct explanation is derived from the lensmaker's formula.
Final Answer
- Assertion: True
- Reason: True, but not the correct explanation for the assertion.
---
The assertion states that the focal length (f) of an equiconvex lens placed in air is equal to the radius of curvature (R) of either face of the lens.
The reason states that for an equiconvex lens, the radius of curvature of both faces is the same. This is indeed true, as an equiconvex lens has two convex surfaces with equal radii of curvature.
The lensmaker's formula is given by:
1f=(μ−1)(1R1−1R2)
where:
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
- Let R1=R (for the first surface),
- Let R2=−R (for the second surface, as per the sign convention).
Substituting these values into the lensmaker's formula:
1f=(μ−1)(1R−(−1R))
1f=(μ−1)(1R+1R)
1f=(μ−1)(2R)
Assuming the refractive index μ=1.5:
1f=(1.5−1)(2R)
1f=0.5(2R)
1f=1R
Taking the reciprocal gives:
f=R
This confirms that the focal length of the equiconvex lens is indeed equal to the radius of curvature of either face.
Thus, both the assertion and the reason are true, but the reason does not correctly explain the assertion. The correct explanation is derived from the lensmaker's formula.
- Assertion: True
- Reason: True, but not the correct explanation for the assertion.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - MULTIPLE CHOICE QUESTIONS
100 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT EXAMPLAR PROBLEMS
11 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
A biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
A1.75B1.33C1.5D1.0
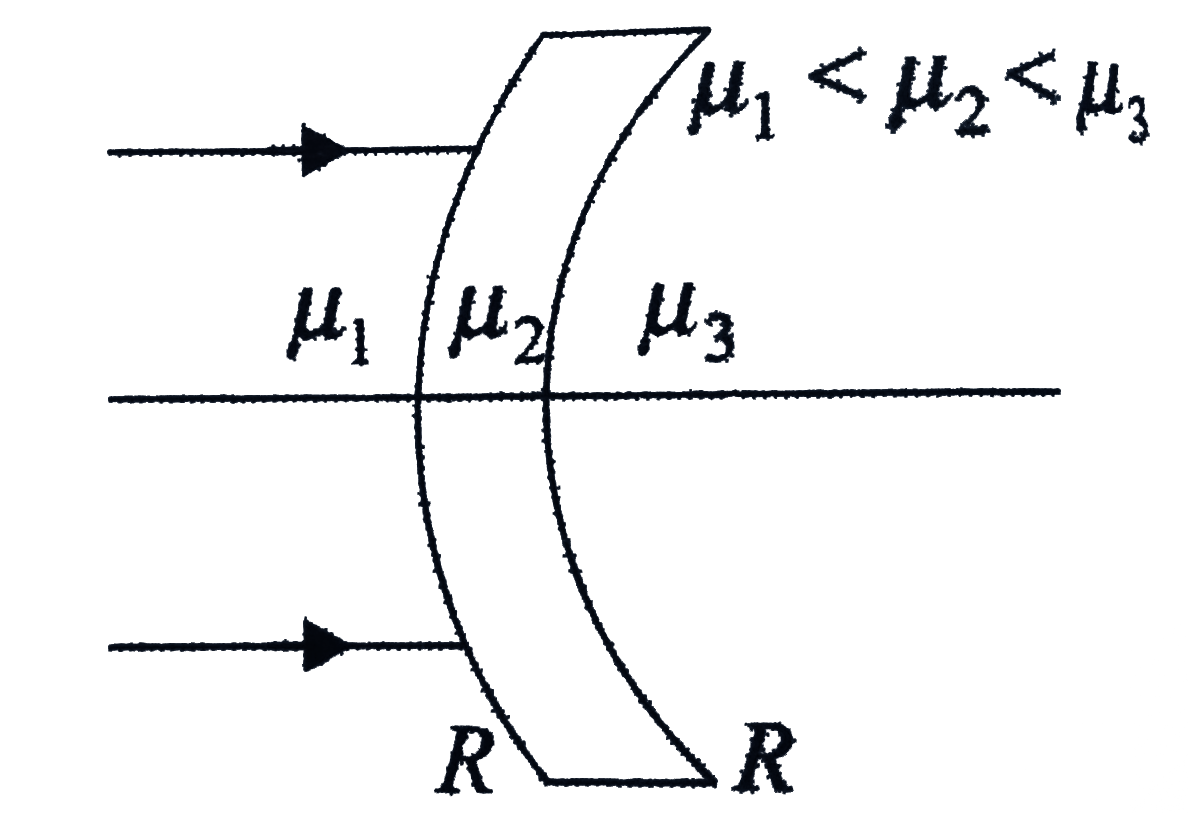
Find the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionThe focal length of a convex mirror is 20 cm its radius of curvature will be
View SolutionA biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View Solution(b) Write the Lens Maker's formula and use it to obtain the range of μ (The refractive index of the material of the lens) for which the focal length of and equiconvex lens, kept in air, would have a greater magnitude than that of the radius of curvature of its two surfaces.
View SolutionThe focal length of an equi-concave lens is 34 times of radius of curvature of its surfaces. Find the refractive index of the material of lens. Under what condition will this lens behave as a converging lens?
View SolutionTwo converging glass lenses A and B have focal lengths in the ratio 2:1. The radius of curvature of first surface of lens A is 1/4 th of the second surface where as the radius of curvature of first surface of lens B is twice that of second surface. Then the ratio between the radii of the first surfaces of A and B is
View Solution
