Assertion : The materials which have very small range of plastic extension are called brittle material.
Reason: If the stress is increased beyond the elastic limit, the material will break.
The correct Answer is:C
To analyze the assertion and reason provided in the question, we will break down the concepts of brittle materials, elastic limit, and the behavior of materials under stress.
1. Understanding the Assertion:
- The assertion states that materials with a very small range of plastic extension are called brittle materials.
- Explanation: Brittle materials exhibit little to no plastic deformation before breaking. When stress is applied, they reach their elastic limit quickly and fail without significant plastic deformation.
2. Understanding the Reason:
- The reason states that if the stress is increased beyond the elastic limit, the material will break.
- Explanation: This statement is generally true for all materials. When stress exceeds the elastic limit, materials can either deform plastically or break, depending on their properties (ductile vs. brittle).
3. Analyzing the Stress-Strain Graph:
- A stress-strain graph can help visualize the behavior of materials under stress.
- Key Points:
- The initial linear portion represents the elastic region where the material will return to its original shape when the stress is removed.
- The point where the material transitions from elastic to plastic deformation is known as the elastic limit.
- Brittle materials will show a very small plastic region and will break shortly after reaching the elastic limit.
4. Conclusion:
- The assertion is correct because brittle materials do have a small range of plastic extension.
- The reason is somewhat misleading because it does not specify which type of material it refers to; it applies to both brittle and ductile materials. Thus, while the statement is true, it is not entirely accurate in the context of the assertion.
Final Answer:
- Assertion: True
- Reason: Partially true but lacks specificity. Therefore, the assertion is correct, but the reason is not adequately explained.
- The assertion states that materials with a very small range of plastic extension are called brittle materials.
- Explanation: Brittle materials exhibit little to no plastic deformation before breaking. When stress is applied, they reach their elastic limit quickly and fail without significant plastic deformation.
- The reason states that if the stress is increased beyond the elastic limit, the material will break.
- Explanation: This statement is generally true for all materials. When stress exceeds the elastic limit, materials can either deform plastically or break, depending on their properties (ductile vs. brittle).
- A stress-strain graph can help visualize the behavior of materials under stress.
- Key Points:
- The initial linear portion represents the elastic region where the material will return to its original shape when the stress is removed.
- The point where the material transitions from elastic to plastic deformation is known as the elastic limit.
- Brittle materials will show a very small plastic region and will break shortly after reaching the elastic limit.
- The assertion is correct because brittle materials do have a small range of plastic extension.
- The reason is somewhat misleading because it does not specify which type of material it refers to; it applies to both brittle and ductile materials. Thus, while the statement is true, it is not entirely accurate in the context of the assertion.
- Assertion: True
- Reason: Partially true but lacks specificity. Therefore, the assertion is correct, but the reason is not adequately explained.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Hooke'S Law
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Assertion The materials having low value of Young's modulus of elasticity are more ductile.
Reason If Young's modulus is less, they can be easily stretched as wires.
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
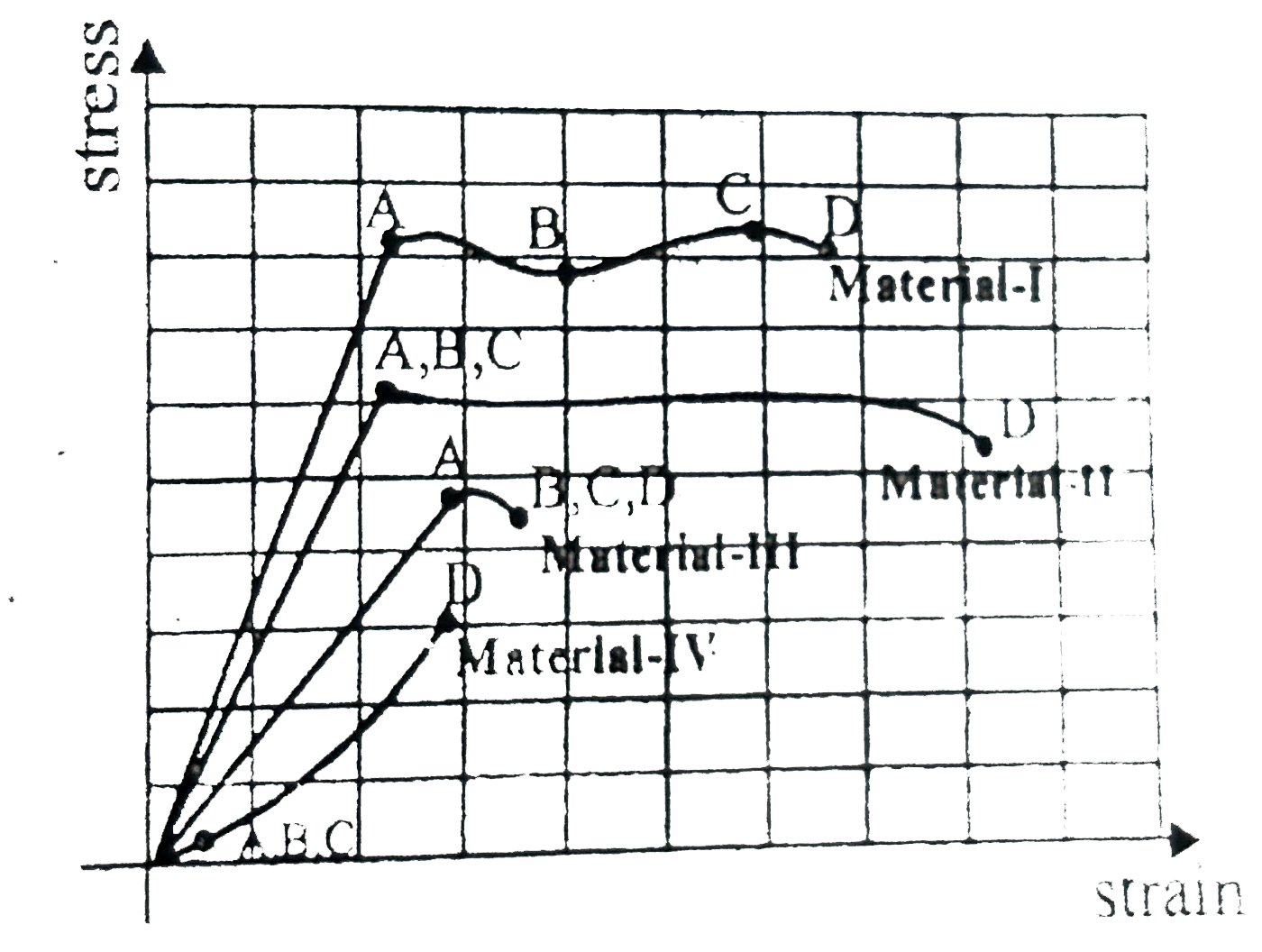
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionAssertion : The maximum height of a mountain on earth can be estimated from the elastic behaviour of rocks.
Reason : At the base of mountain, the pressure less than elastic limit of earths supporting material.
View SolutionTwo bars A and B of circular cross section, same volume and made of the same material, are subjected to tension. If the diameter of A is half that of B and if the force applied to both the rod is the same and it is in the elastic limit, the ratio of extension of A to that of B will be
View SolutionMaterials get deformed when force is applied. Some of them regain their status when the applied force is removed. They are termed as elastic. Those of which not regaining are called plastic. There may be delay in the regaining in some materials. They are said to have got elastic aftereffect, since they have gone beyond the elastic limit. Repeated application and removal of force leads to fatigueness in the material. Fatigued materials may break at any point time and so are avoided.
The stress strain graph for two materials A and B is shown in the following figure:
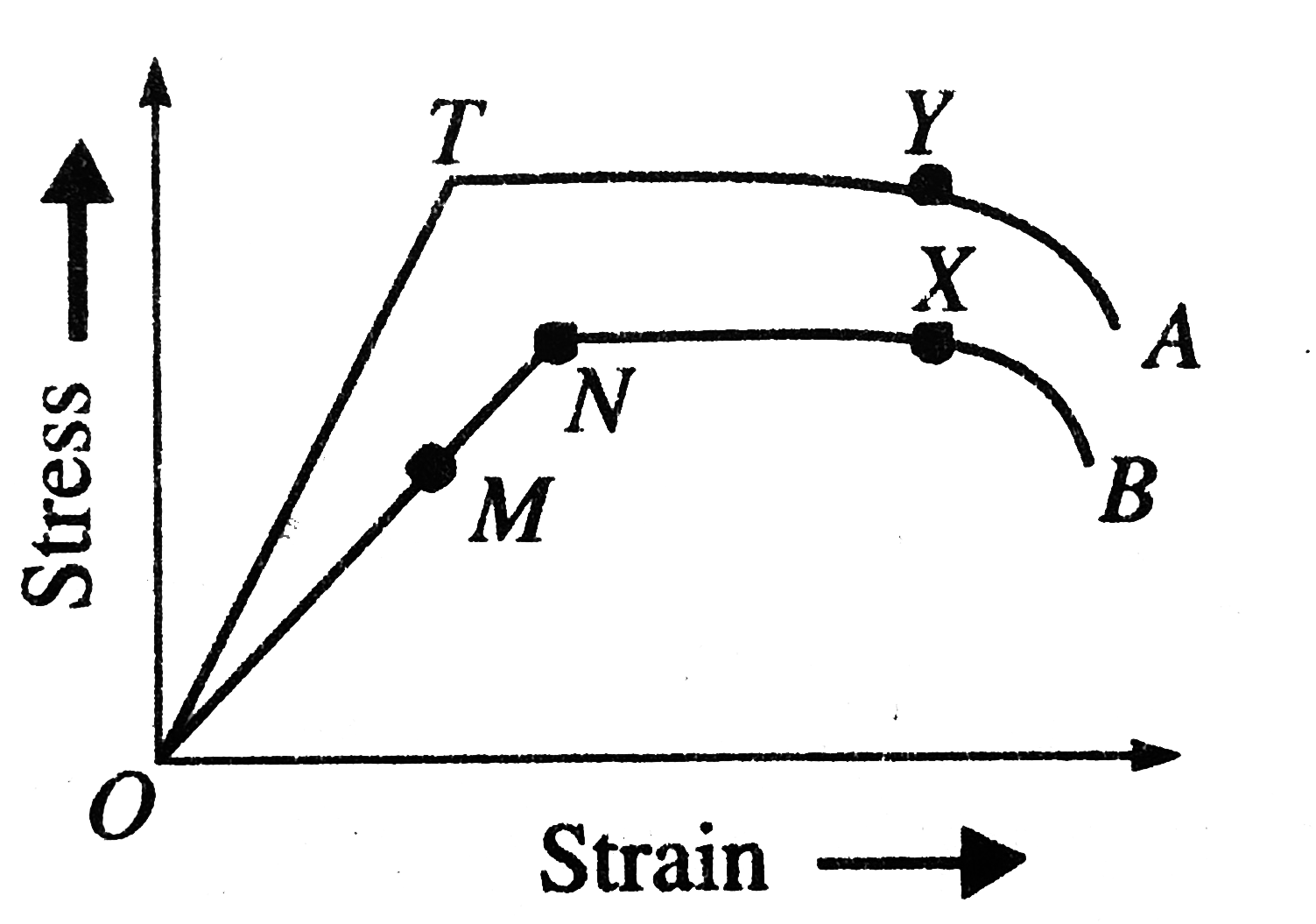
The time in which the two materials regain their original status is tA and tB related as tB=2tB. Then the material under elastic aftereffect (relatively) is
View SolutionMaterials get deformed when force is applied. Some of them regain their status when the applied force is removed. They are termed as elastic. Those of which not regaining are called plastic. There may be delay in the regaining in some materials. They are said to have got elastic aftereffect, since they have gone beyond the elastic limit. Repeated application and removal of force leads to fatigueness in the material. Fatigued materials may break at any point time and so are avoided.
The stress strain graph for two materials A and B is shown in the following figure:

The strength of the material A and B is SA and SB, respectively, while the longevity of plastic behaviour is LA and LB. Then
View SolutionMaterials get deformed when force is applied. Some of them regain their status when the applied force is removed. They are termed as elastic. Those of which not regaining are called plastic. There may be delay in the regaining in some materials. They are said to have got elastic aftereffect, since they have gone beyond the elastic limit. Repeated application and removal of force leads to fatigueness in the material. Fatigued materials may break at any point time and so are avoided.
The stress strain graph for two materials A and B is shown in the following figure:
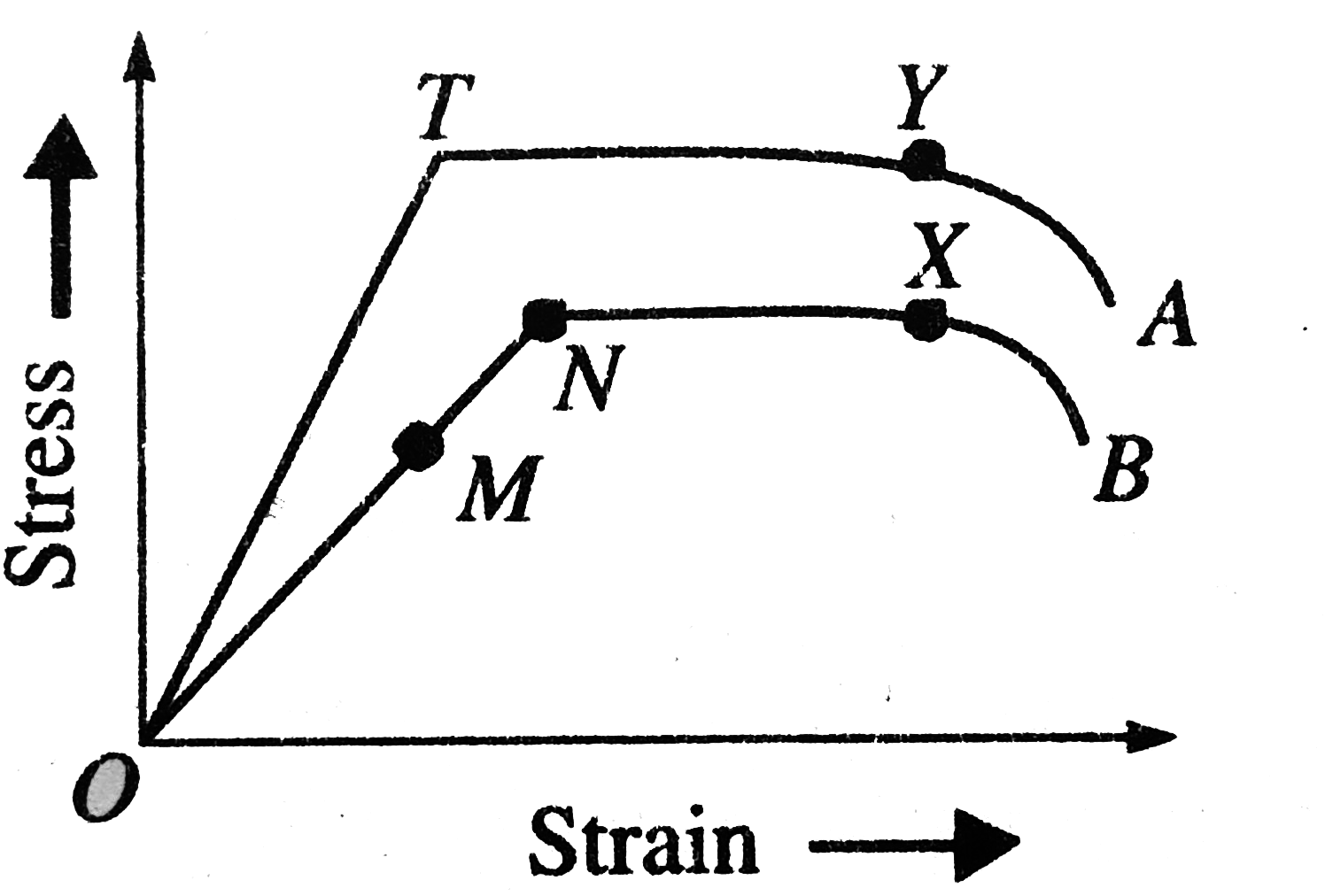
If the intensity of A and B is EA and EB, respectively
View Solution
