Assertion : When the orbital radius of a planet is made 4 times, its time period increases by 8 times
Reason : Greater the height above the Earth's surface, greater is the time period of revolution
Both A and are true and R is correct explanation of the assertion
Both A and R are true but R is not the correct explanation of the assertion
A is true, but R is false .
A is false, but R is true
The correct Answer is:B
To solve the assertion and reason question, we need to analyze both the assertion and the reason using Kepler's third law of planetary motion. Here’s a step-by-step solution:
Step 1: Understand the Assertion
The assertion states that when the orbital radius of a planet is made 4 times larger, its time period increases by 8 times.
Step 2: Apply Kepler's Third Law
According to Kepler's third law, the square of the time period (T) of a planet is directly proportional to the cube of the orbital radius (R) of the planet:
T2∝R3
This can be expressed mathematically as:
T21T22=R31R32
Step 3: Set Up the Ratios
Let’s denote the initial radius as R1 and the new radius as R2=4R1. Let T1 be the initial time period and T2 be the new time period. According to the assertion, we need to check if T2=8T1.
Step 4: Substitute the Values
Substituting R2 into the equation:
T21T22=R31(4R1)3
This simplifies to:
T21T22=R3164R31=164
Step 5: Solve for T22
Cross-multiplying gives:
T21=164T22
Rearranging gives:
T22=64T21
Taking the square root of both sides:
T2=8T1
Thus, the assertion is correct.
Step 6: Understand the Reason
The reason states that the greater the height above the Earth's surface, the greater the time period of revolution. This is also true because as the height increases, the orbital radius increases, leading to a longer time period.
Step 7: Conclusion on the Reason
While both the assertion and reason are correct, the reason does not specifically explain the assertion. It does not mention Kepler's third law, which is the fundamental principle behind the relationship between orbital radius and time period.
Final Answer
Both the assertion and reason are true, but the reason is not the correct explanation of the assertion.
The assertion states that when the orbital radius of a planet is made 4 times larger, its time period increases by 8 times.
According to Kepler's third law, the square of the time period (T) of a planet is directly proportional to the cube of the orbital radius (R) of the planet:
T2∝R3
This can be expressed mathematically as:
T21T22=R31R32
Let’s denote the initial radius as R1 and the new radius as R2=4R1. Let T1 be the initial time period and T2 be the new time period. According to the assertion, we need to check if T2=8T1.
Substituting R2 into the equation:
T21T22=R31(4R1)3
This simplifies to:
T21T22=R3164R31=164
Cross-multiplying gives:
T21=164T22
Rearranging gives:
T22=64T21
Taking the square root of both sides:
T2=8T1
Thus, the assertion is correct.
The reason states that the greater the height above the Earth's surface, the greater the time period of revolution. This is also true because as the height increases, the orbital radius increases, leading to a longer time period.
While both the assertion and reason are correct, the reason does not specifically explain the assertion. It does not mention Kepler's third law, which is the fundamental principle behind the relationship between orbital radius and time period.
Both the assertion and reason are true, but the reason is not the correct explanation of the assertion.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS CBSE BOARDEXERCISE - Section - B12videos
FOOTSTEPS TOWARDS CBSE BOARD
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS CBSE BOARDEXERCISE - Section - C16videos
FOOTSTEPS TOWARDS CBSE BOARD
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS JEE MAIN EXERCISE - Section B (Numerical Value Type Questions)10videos
FOOTSTEPS TOWARDS JEE MAIN
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question45videos
FOOTSTEPS TOWARDS NEET
Similar Questions
A simple pendulum has a time period 2 s on the earth surface. If pendulum is taken to height R2 above the earth 's surface, (R is radius of the earth), the time period becomes
View SolutionThe Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
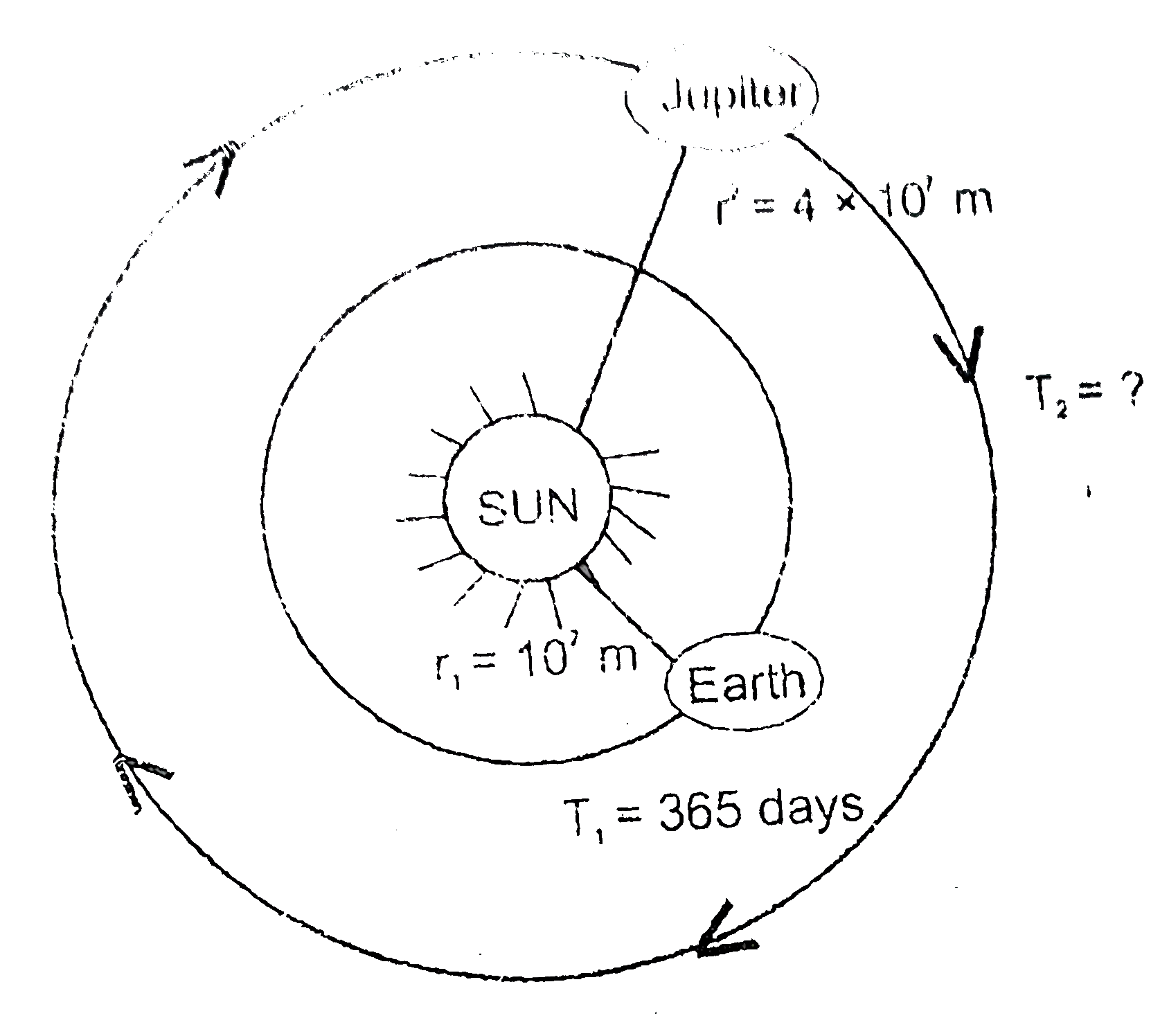 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Satellite revolving around the earth at a height of 400 Km above the earth's surface has a time period of about
A24 hoursB90 minutesC2 hoursD>24 hours - Question 2 - Select One
The radius of orbit of a planet is two times that of the earth. The time period of planet is
A4.2 yearsB2.8 yearsC5.6 yearsD8.4 years - Question 3 - Select One
A simple pendulum has a time period T1 on the surface of earth of radius R. When taken to a height of R above the earth's surface, its time period is T2, ratio T2T is
A1√2B√2C2D4
Radius of orbit of a satellite is R and T is time period. Find T' when orbit radius increase to 9R
View SolutionRadius of orbit of a satellite is R and T is time period. Find T' when orbit radius increase to 9R
View SolutionAssertion : When a simple pendulum is made to oscillate on the surface of moon , its time period increase
Reason: Moon is much smaller compared to earthView SolutionA body is projected from earth's surface to become its satellite, its time period of revolution will not depend upon
View SolutionThe time period of a simple pendulum is 2s. It its length is increased by 4 times, then its period becomes
View Solution
