Assume the radius of the earth to be 6.4×106m
a. Calculate the time period T of a satellite on equational orbit at 1.4×10em above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?
a. r=Rearth+h=6.4×106+1.4×106=7.8×106m
⇒r=7.8×106m⇒T=(4π2r3GMearth)=6831s
b. Speed of satellite
V=√GMearthr=7174ms−1
c. Relative angular velocity =ωsatellite−ωearth
Thus T=2πωs−ωe=2π[2πTs−2πTe]
⇒T=TsTeTe−Ts=7471s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.113videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.215videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A satellite having time period of revolution 6830 sec is travelling in the same direction as the rotation of the earth, i.e. from west to east, the time interval between the two successive times at which it will appear vertically overhead to an observer at a fixed point on the equator is
View SolutionA satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is:
View Solution
Knowledge Check
- Question 1 - Select One
Match the Column I with Column II
For a satellite in circular orbit
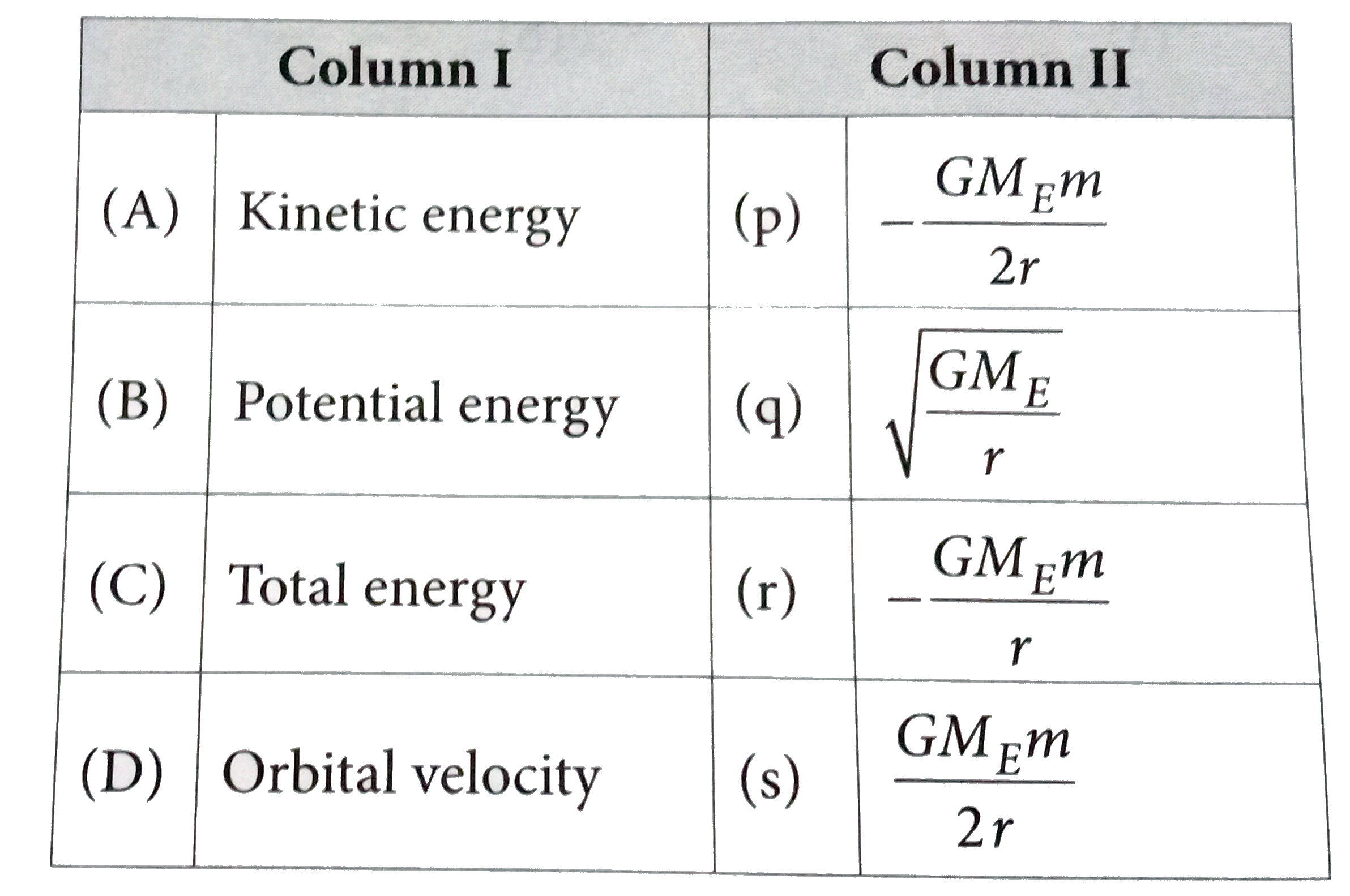
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )AA-r, B-s,C-q,D-pBA-q,B-p,C-r,D-sCA-p,B-q,C-s,D-rDA-s,B-r,C-p,D-q - Question 2 - Select One
A geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
A3√2hB1.5√2hC6√2hD12√2h
A satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is:
View SolutionA satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is:
View SolutionA geostationary satellite is orbiting the earth at a height of 5R above the surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R form the surface of the earth is
View SolutionA geostationary satellite is orbiting the earth at a height of 5R above the surface of the earth, 2R being the radius of the earth. The time period of another satellite in hours at a height of 2R form the surface of the earth is
View SolutionThe time period of a satellite in a circular orbit around the earth is T . The kinetic energy of the satellite is proportional to T−n . Then, n is equal to :
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View Solution

