At one instant, the centre of mass of a system of two particles is located on the x-axis at x=3.0m and has a velocity of (6.0m/s)ˆj. One of the particles is at the origin, the other particle has a mass of 0.10kg and is at rest on the x−axis at x=12.0m.
(a) What is the mass of the particle at the origin?
(b) Calculate the total momentum of this system.
(c) What is the velocity of the particle at the origin?
The correct Answer is:A, B, C, D
(a) xCM=m1x1+m2x2m1+m2
⇒3=m1(0)+(0.10)(12)m1+0.1
Solving this equation we get,
=m1+0.3kg
(b) PCM=mCMvCM
=(0.1+0.3)(6ˆj)
=(2.4ˆj)kg⋅m/s
(c) PCM=P1+P2
∴(2.4ˆj)=(0.3)v1+(0.1)(0)
∴v1=(8ˆj)m/s
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.3
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Centre of mass of two particles with masses 1kg and 2kg located at (2,0,2) and (1,1,0) has the co-ordinates of ?
View SolutionA system consists of two particles. At t=0, one particle is at the origin, the other, which has a mass of 0.60kg, is on the y-axis at y=80m. At t=0, the centre of mass of the system is on the y−aξs at y=24m and has a velocity given by (6.0m/s3)t2ˆj.
(a) Find the total mass of the system.
(b) Find the acceleration of the centre of mass at any time t.
(c) Find the next external force acting on the system at t=3.0s.
View Solution
Knowledge Check
Vx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0m
A particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin OAremains constantBcontinuously increasesCcontinuously decreasesDoscillates.vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
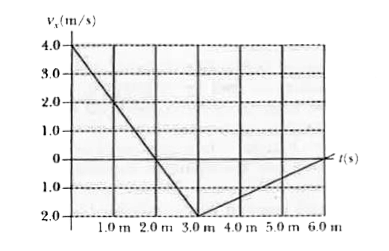 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A particle of mass 0.01 kg having position vector →r=(10ˆi+6ˆj) meters is moving with a velocity 5ˆim/s . Calculate its angular momentum about the origin.
View SolutionA body has its centre of maas at the origin. The x-coordinates of the particles
View SolutionTwo particles, A and B of masses m and 3m, are moving along X and Y axes respectively, with the same speed v. They collide at the origin, and coalesce into one body, after the c ollision. What is the velocity of this coalesced mass ?
View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View SolutionConsider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View Solution
