At which position the kinetic energy of a harmonic oscillator is maximum or minimum ?
To determine at which position the kinetic energy of a harmonic oscillator is maximum or minimum, we can follow these steps:
Step 1: Understand the Motion of a Harmonic Oscillator
A harmonic oscillator undergoes simple harmonic motion (SHM), which can be described by the equation:
y=Asin(ωt)
where:
- y is the displacement from the mean position,
- A is the amplitude,
- ω is the angular frequency,
- t is time.
Step 2: Identify Key Positions
In SHM, there are two key positions:
- Mean Position: where the displacement x=0.
- Extreme Positions: where the displacement is at maximum, x=A or x=−A.
Step 3: Write the Expression for Kinetic Energy
The kinetic energy KE of the harmonic oscillator can be expressed as:
KE=12mv2
where m is the mass and v is the velocity of the oscillator.
Step 4: Relate Velocity to Displacement
To find the velocity in terms of displacement, we differentiate the displacement function:
v=dydt=Aωcos(ωt)
Using the relationship v2=(Aωcos(ωt))2, we can express kinetic energy in terms of displacement.
Step 5: Substitute for Velocity in Kinetic Energy
To express kinetic energy in terms of position x, we can use the relationship:
v=ω√A2−x2
Thus, substituting this into the kinetic energy formula gives:
KE=12m(ω√A2−x2)2=12mω2(A2−x2)
Step 6: Determine Maximum and Minimum Kinetic Energy
- Maximum Kinetic Energy: This occurs when x=0:
KEmax=12mω2A2
- Minimum Kinetic Energy: This occurs at the extreme positions x=A or x=−A:
KEmin=0
Conclusion
The kinetic energy of a harmonic oscillator is maximum at the mean position (x=0) and minimum at the extreme positions (x=A or x=−A).
---
A harmonic oscillator undergoes simple harmonic motion (SHM), which can be described by the equation:
y=Asin(ωt)
where:
- y is the displacement from the mean position,
- A is the amplitude,
- ω is the angular frequency,
- t is time.
In SHM, there are two key positions:
- Mean Position: where the displacement x=0.
- Extreme Positions: where the displacement is at maximum, x=A or x=−A.
The kinetic energy KE of the harmonic oscillator can be expressed as:
KE=12mv2
where m is the mass and v is the velocity of the oscillator.
To find the velocity in terms of displacement, we differentiate the displacement function:
v=dydt=Aωcos(ωt)
Using the relationship v2=(Aωcos(ωt))2, we can express kinetic energy in terms of displacement.
To express kinetic energy in terms of position x, we can use the relationship:
v=ω√A2−x2
Thus, substituting this into the kinetic energy formula gives:
KE=12m(ω√A2−x2)2=12mω2(A2−x2)
- Maximum Kinetic Energy: This occurs when x=0:
KEmax=12mω2A2
- Minimum Kinetic Energy: This occurs at the extreme positions x=A or x=−A:
KEmin=0
The kinetic energy of a harmonic oscillator is maximum at the mean position (x=0) and minimum at the extreme positions (x=A or x=−A).
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Additional Question )
3 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (fill in the blanks)
9 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - HOTS (Higher Order Thinking Skills & Advanced Level)
11 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Knowledge Check
The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
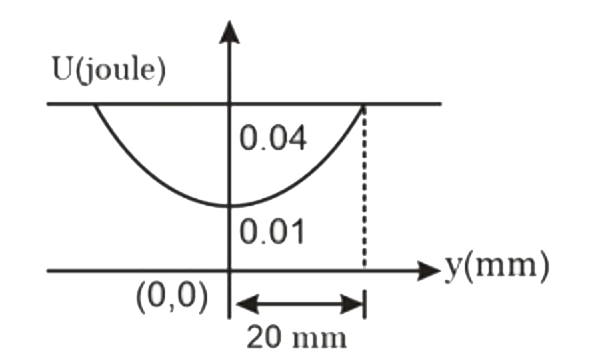 A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1
A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1Find the average kinetic energy of a simple harmonic oscillator if its total energy is 10 joule and minimum potential energy is 2 joule.
A1JB4JC8JD5JIf the potential energy of a harmonic oscillator of mass 2kg on its equilbrium position is 5 joules and the total energy is 9 joules when the amplitude is one meter the period of the oscillator ("in" sec) is-
A1.5B3.14C6.28D4.67
A particle executes simple harmonic motion of ampliltude A. At what distance from the mean position is its kinetic energy equal to its potential energy?
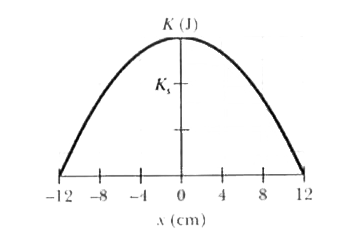
View SolutionFigure 15.39 shows the kinetic energy K of a simple harmonic oscillator versus its position x. The vertical axis scale is set by Ks=8.0J. What is the spring constant?
View SolutionCalculate the maximum kinetic energy of a linear harmonic oscillator of force constant 12×105 N/m., amplitude 0.05 m.
View SolutionThe average kinetic energy of a simple harmonic oscillator is 2 joule and its total energy is 5 joule. Its minimum potential energy is
View SolutionAn object of mass 0.2kg execurtes Simple harmonic along X-axis with frequncey of 25πHz. At the position x=0.04 m, the object has kinetic energy of oscillation in meter is equal to
View Solution
