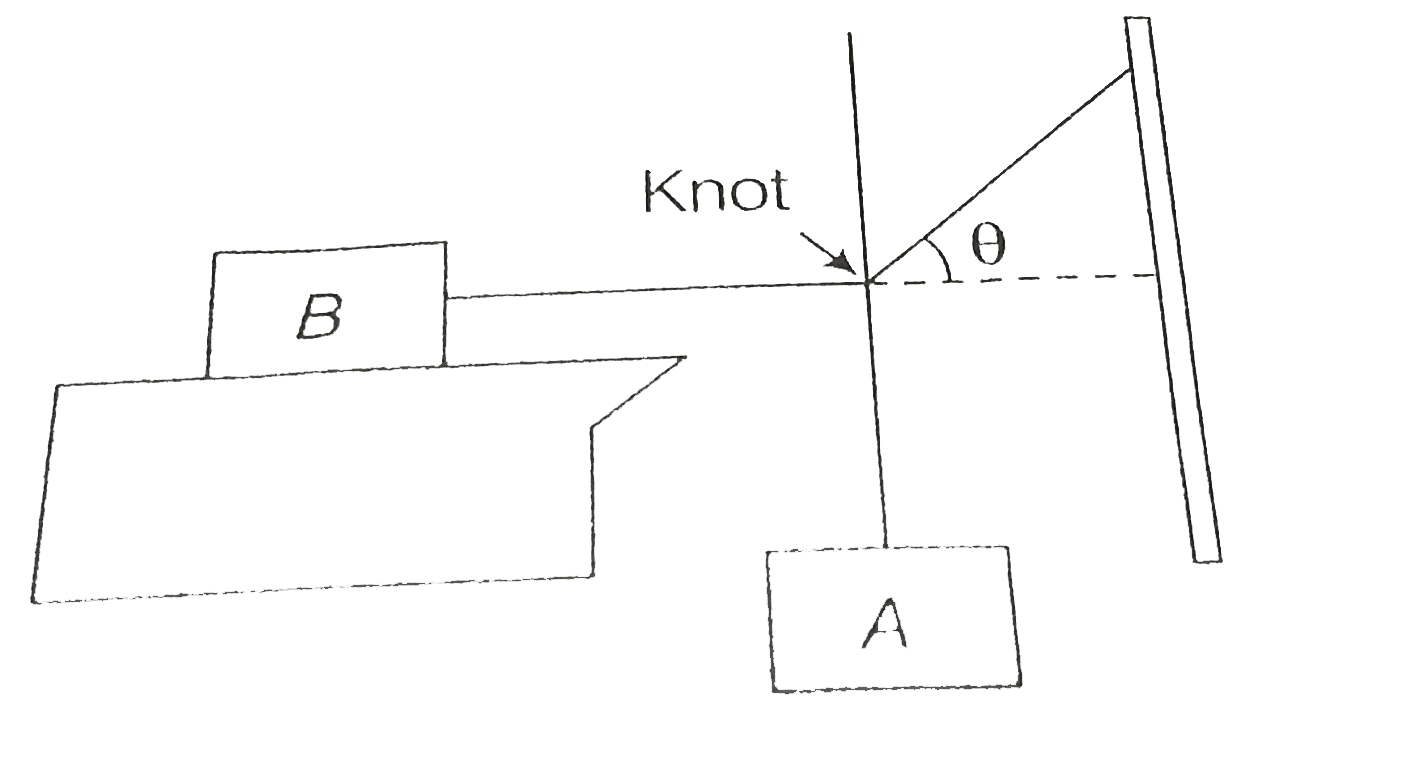
Block B in Fig. 6-12 weighs 711 N. The coefficient of static friction between block and table is 0.25 angle θ is 30∘, assume that the cord between B and the knot is horizontal. Find the maximum weight of block A for which the system will be stationary.

Figure 6-12 A block hanging from a knotted position.
In order that the two blocks remain in equilibrium, friction must be present between block B and the surface.
In order that the two blocks remain in equilibrium, friction must be present between block B and the surface. Reasoning: The free-body diagrams for block B and for the knot just above block A is shown in Fig. 6-13. In this case, →T1 is the tension force of the rope pulling on block B or pulling on the knot (as the case may be), →T2 is the

Figure 6-13 The free-body diagrams for block B and for the knot just above block A.
tension force exerted by the second rope (at angle θ=30∘) on the knot, →f is the force of static friction exerted by the horizontal surface on block B,→FN is normal force exerted by the surface on block B,WA s the weight of block A ( WA is the magnitude of mA→g) and WB is the weight of block B (WB)=711N is the magnitude of mB→g).
Calculations: For each object, we take +x horizontally rightward and +y upward. Applying Newton.s second law in the x- and y-directions for block B and then doing the same for the knot results in four equations:
T1−fs.max=0,
FN−WB=0,
T2cosθ−T1=0,
T2cosθ−T1=0,
T2sinθ−WA=0,
where we assume the static friction to be at its maximum value (permitting us to use Eq. 6-1). The above equations yield T1=μsFN,FN=WBandT1=T2cosθ.
Solving these equations with μs=0.25, we obtain
WA=T2sinθ=T1tanθ=μsFNtanθ=μsWBtanθ
=(0.25)(711N)tan30∘=1.0×102N
As expected, the maximum weight of A is proportional to the weight of B, as well as the coefficient of static friction. In addition, we see that WA is proportional to tan θ (the larger the angle, the greater the vertical component of T2 that supports its weight).
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS5videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
 View Solution
View Solutiona. Block A , as shown in figure weight 60.0N The coefficient of static friction between the block and the surface on which it rest is 0.25 .The system is in equlibrium .Find the friction for excerted on block A
b. Find the maximum weight w for which the system will remain in equlibrium View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Block B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
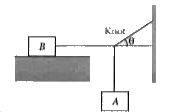 AWtanθμBμWtanθCμW√1+tan2θDμWsinθ
AWtanθμBμWtanθCμW√1+tan2θDμWsinθ - Question 2 - Select One
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
 AwtanθμBμwtanθCμw√1+tan2θDμwsinθ
AwtanθμBμwtanθCμw√1+tan2θDμwsinθ - Question 3 - Select One
Block B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is
 A3/7ms−2B4/3ms−2C6/7ms−2D3/2ms−2
A3/7ms−2B4/3ms−2C6/7ms−2D3/2ms−2
Block A in figure weights 90 N. The coefficient of static friction between the block and the surface on which it rests is 0.3. The weight w is 15N, and the system is in equilibrium. Find the friction force exerted on block A.(b) Find the maximum weight w for which the system will remain in equilibrium.
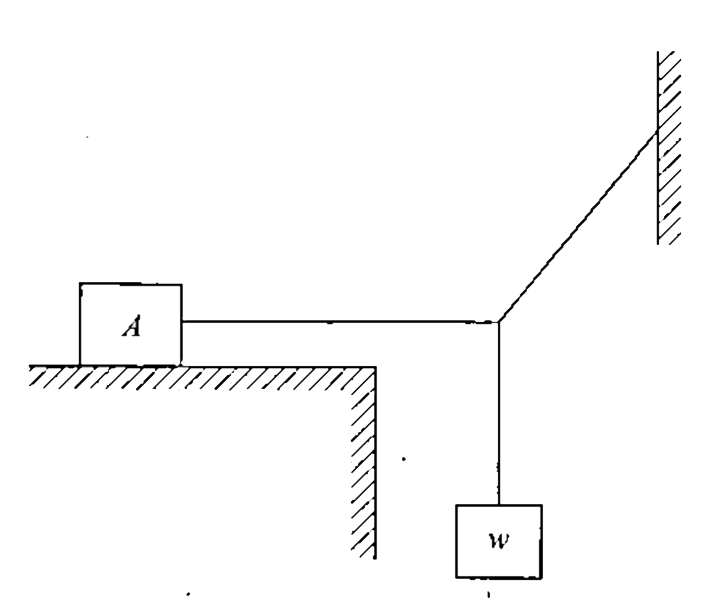 View Solution
View Solutiona. Block A , as shown in figure weight 60.0N The coefficient of static friction between the block and the surface on which it rest is 0.25 .The waight w is 12N The system is in equlibrium .Find the friction for excerted on block A
b. Find the maximum weight w for which the system will remain in equlibrium View Solution
View SolutionThe breaking strength of the string connecting wall and block B is 175 N, find the magnitude of weight of block A for which the system will be stationary. The block B weighs 700 N.
(g=10m/s2)
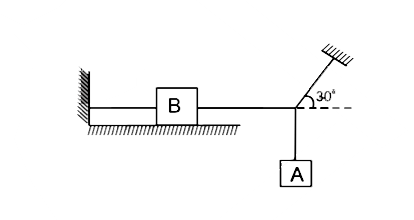 View Solution
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isView SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isView Solution

