Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

As the blocks move , the spring is extended.
Due to the force , speed of 2m decreases and that of m increases. At the time of maximum elongation , the block moves with same veloctiy .
x0: maximum elongation
m×0+2mv0=mv+2mv
⇒v=2v03
12×2mv20=12(m+2m)v2+12kx20
x0=√2mv203k=v0√2m3k
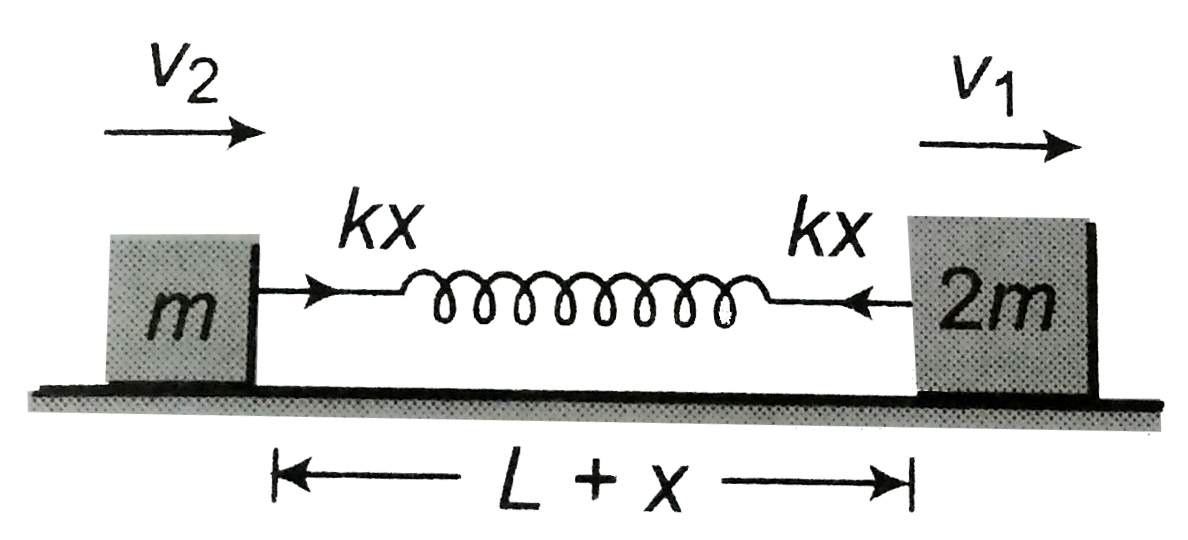

Topper's Solved these Questions
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View Solution
Knowledge Check
An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2kA ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
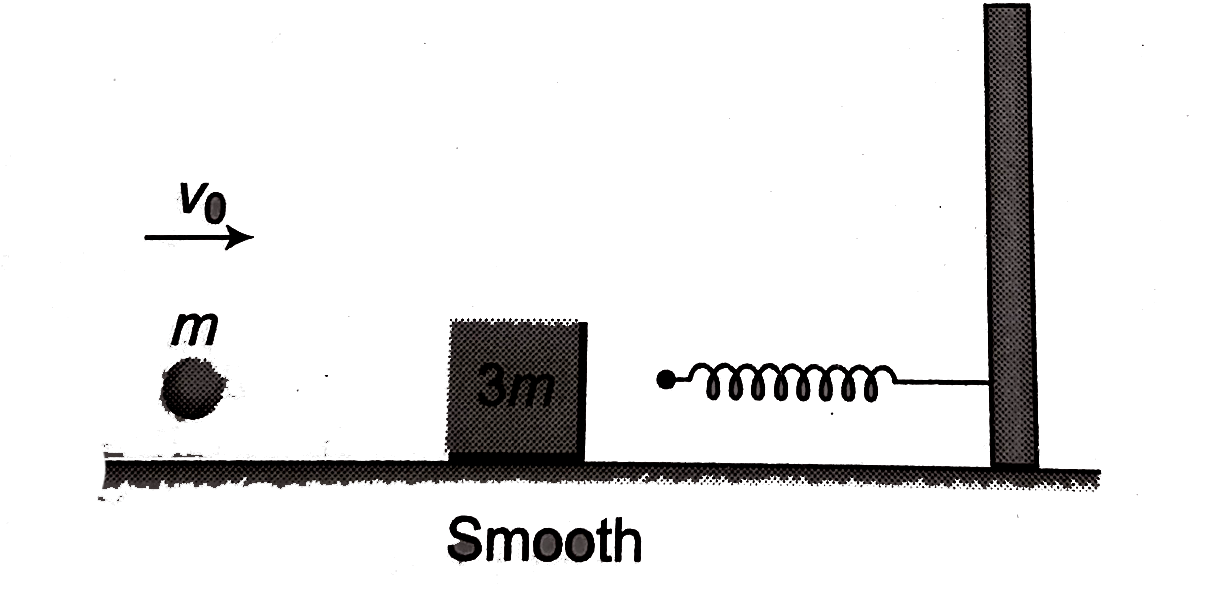 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204kA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
 AmakB12makC2makD124mak
AmakB12makC2makD124mak
A particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring

View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View Solution
