Boiling water: Suppose 1.0 g of water vaporizes isobarically at atmospheric pressure (1.01×105Pa). Its volume in the liquid state is Vi=Vliquid=1.0cm3 and its volume in vapour state is Vf=Vvapour=1671cm3. Find the work done in the expansion and the change in internal energy of the system. Ignore any mixing of the stream and the surrounding air. Take latent heat of vaporization Lv=2.26×106J/kg.
The correct Answer is:A, B
To solve the problem step by step, we will calculate the work done during the vaporization of water and the change in internal energy of the system.
Step 1: Calculate the Work Done in Expansion
The work done W during an isobaric process is given by the formula:
W=P×(Vf−Vi)
Where:
- P is the pressure (in Pascals)
- Vf is the final volume (in cubic meters)
- Vi is the initial volume (in cubic meters)
Given:
- P=1.01×105Pa
- Vi=1.0cm3=1.0×10−6m3
- Vf=1671cm3=1671×10−6m3
Now, substituting the values into the work done formula:
W=1.01×105Pa×(1671×10−6m3−1.0×10−6m3)
Calculating the difference in volume:
Vf−Vi=1671×10−6−1.0×10−6=1670×10−6m3
Now substituting back:
W=1.01×105×1670×10−6
Calculating W:
W=1.01×1670×10−1=168.67J≈169J
Step 2: Calculate the Change in Internal Energy
According to the first law of thermodynamics:
Q=ΔU+W
Where:
- Q is the heat added to the system
- ΔU is the change in internal energy
- W is the work done by the system
The heat added Q during the phase change can be calculated using the formula:
Q=m×Lv
Where:
- m is the mass (in kg)
- Lv is the latent heat of vaporization
Given:
- m=1.0g=1.0×10−3kg
- Lv=2.26×106J/kg
Calculating Q:
Q=1.0×10−3kg×2.26×106J/kg=2260J
Now substituting Q and W into the first law equation to find ΔU:
2260=ΔU+169
Rearranging to solve for ΔU:
ΔU=2260−169=2091J
Final Answers
- Work done W = 169 J
- Change in internal energy ΔU = 2091 J
The work done W during an isobaric process is given by the formula:
- P is the pressure (in Pascals)
- Vf is the final volume (in cubic meters)
- Vi is the initial volume (in cubic meters)
- P=1.01×105Pa
- Vi=1.0cm3=1.0×10−6m3
- Vf=1671cm3=1671×10−6m3
According to the first law of thermodynamics:
- Q is the heat added to the system
- ΔU is the change in internal energy
- W is the work done by the system
- m is the mass (in kg)
- Lv is the latent heat of vaporization
- m=1.0g=1.0×10−3kg
- Lv=2.26×106J/kg
- Work done W = 169 J
- Change in internal energy ΔU = 2091 J
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 2
1 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 3
1 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
One gram of water (1cm3) becomes 1671cm3 of steam when boiled at a constant pressure of 1 atm (1.013×105Pa). The heat of vaporization at this pressure is Lv=2.256×106J/kg. Compute (a) the work done by the water when it vaporizes and (b) its increase in internal energy.
View SolutionOne gram of water (1cm3) becomes 1671cm3 of steam when boiled at a constant pressure of 1 atm (1.013×105Pa). The heat of vaporization at this pressure is Lv=2.256×106J/kg. Compute (a) the work done by the water when it vaporizes and (b) its increase in internal energy.
View SolutionUnit mass of liquid of volume V1 completely turns into a gas of volume V2 at constant atmospheric pressure P and temperature T. The latent heat of vaporization is "L". Then the change in internal energy of the gas is
View SolutionAt 1 atmospheric pressure, 1.000 g of water having a volume of 1.000cm3 becomes 1671 cm3 of steam when boiled. The heat of vaporization of water at 1 atmosphere is 539cal/g . What is the change in internal energy during the process ?
View SolutionCalculate the entropy change when one mole of water at 373 K is converted into steam. Latent heat of vaporisation of water (ΔHv) is 40.7×103Jmol−1
View SolutionOne mole of an ideal gas is heated isobarically from the freezing point to the boiling point of water, each under normal pressure. Find out the work done by the gas and the change in its internal energy. The amount of heat involved is 1 kJ. Given gas constant R= 8.3 J/mol K.
View SolutionAt 100∘C and 1 atm, if the density of the liquid water is 1.0gcm−3 and that of water vapour is 0.00006gcm−3 , then the volume occupied by water molecules in 1L steam at this temperature is
View Solution1kg ice at 0∘C is mixed with 1kg of steam at 100∘C. What will be the composition of the system when thermal equilibrium is reached ? Latent heat of fusion of ice =3.36×106Jkg−1 and latent heat of vaporization of water =2.26×106Jkg−1
View SolutionA sample of 0.1g of water of 100∘C and normal pressure (1.013×105Nm−2) requires 54 cal of heat energy to convert to steam at 100∘C. If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample is
View SolutionA thermodynamical process is shown in the figure with pA=3×patm, VA=2×10−4m3, pB=8×patm, VC=5×10−4m3. In the process AB and BC, 600J and 200J heat are added to the system. Find the change in internal energy of the system in the process CA. [1patm=105N/m2]
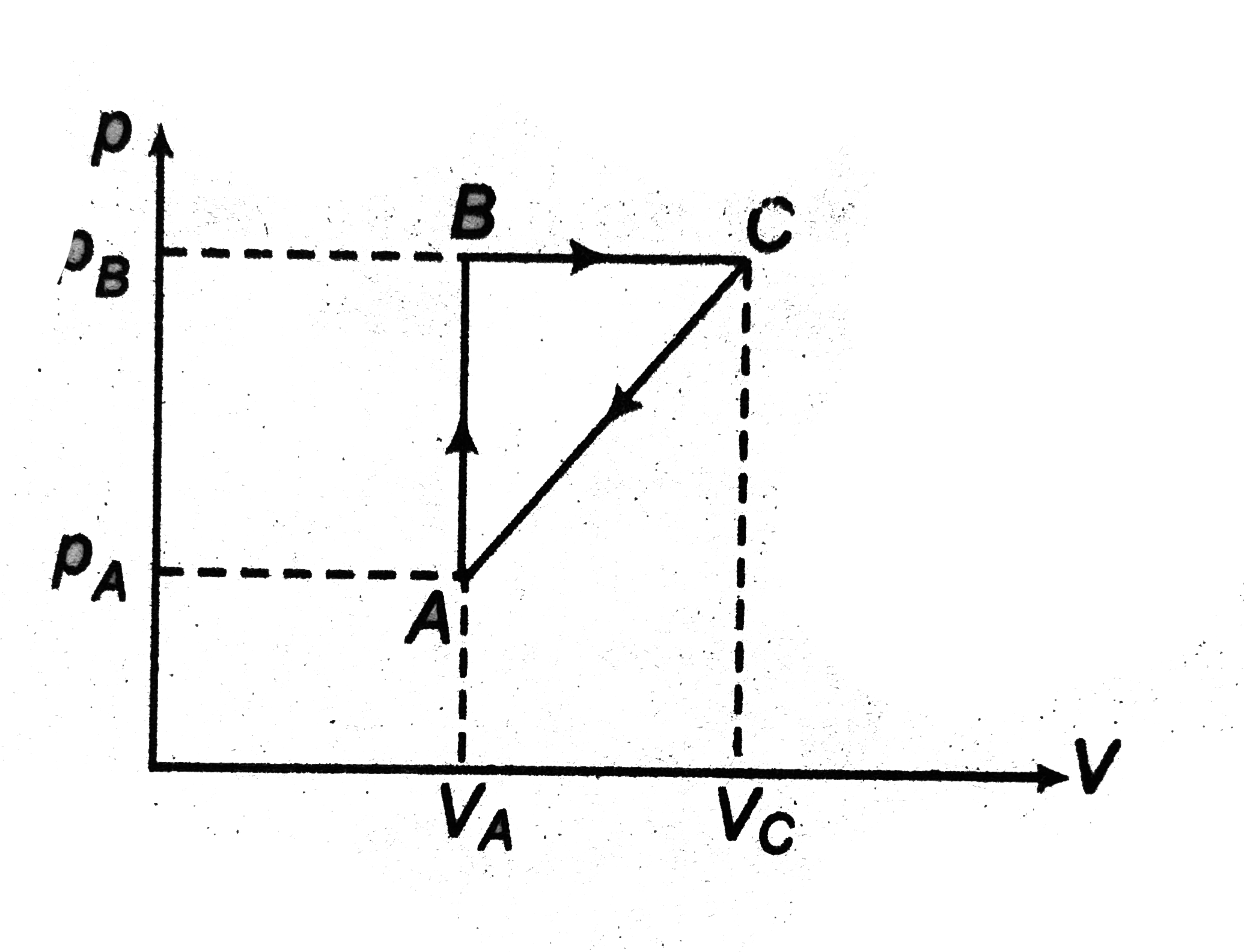
View Solution
