Boojho was riding in his bicycle along a straight road. He classified the motion of various parts of the bicycle as (i) rectilinear motion, (ii) circular motion and (iii) both rectilinear as well as circular motion. Can you list one part of the bicycle for each type of motion? Support your answer with reason.
Step-by-Step Solution:
1. Understanding Rectilinear Motion:
- Rectilinear motion refers to motion along a straight line. In the context of a bicycle, we can identify parts that move in a straight line when the bicycle is in motion.
Part of the Bicycle:
- Seat of the Bicycle
- Reason: The seat remains fixed in a straight line as the bicycle moves forward. When a rider sits on the seat, it does not change its position in any direction other than straight ahead.
2. Understanding Circular Motion:
- Circular motion refers to motion along a circular path. This type of motion can be observed in parts of the bicycle that rotate around a fixed point.
Part of the Bicycle:
- Pedals of the Bicycle
- Reason: The pedals rotate around the axis of the crankset, creating circular motion as they are pushed down and pulled up by the rider's feet.
3. Understanding Both Rectilinear and Circular Motion:
- Some parts of the bicycle exhibit both types of motion simultaneously. This occurs when a part moves forward while also rotating around an axis.
Part of the Bicycle:
- Wheels of the Bicycle
- Reason: The wheels rotate around their own axis (circular motion) while also moving forward along the road (rectilinear motion). This combination allows the bicycle to travel straight while the wheels are continuously turning.
Summary of Parts and Motions:
- Rectilinear Motion: Seat of the Bicycle (moves in a straight line)
- Circular Motion: Pedals of the Bicycle (rotate around an axis)
- Both Rectilinear and Circular Motion: Wheels of the Bicycle (rotate and move forward)
- Rectilinear motion refers to motion along a straight line. In the context of a bicycle, we can identify parts that move in a straight line when the bicycle is in motion.
- Seat of the Bicycle
- Reason: The seat remains fixed in a straight line as the bicycle moves forward. When a rider sits on the seat, it does not change its position in any direction other than straight ahead.
- Circular motion refers to motion along a circular path. This type of motion can be observed in parts of the bicycle that rotate around a fixed point.
- Pedals of the Bicycle
- Reason: The pedals rotate around the axis of the crankset, creating circular motion as they are pushed down and pulled up by the rider's feet.
- Some parts of the bicycle exhibit both types of motion simultaneously. This occurs when a part moves forward while also rotating around an axis.
- Wheels of the Bicycle
- Reason: The wheels rotate around their own axis (circular motion) while also moving forward along the road (rectilinear motion). This combination allows the bicycle to travel straight while the wheels are continuously turning.
- Rectilinear Motion: Seat of the Bicycle (moves in a straight line)
- Circular Motion: Pedals of the Bicycle (rotate around an axis)
- Both Rectilinear and Circular Motion: Wheels of the Bicycle (rotate and move forward)
Topper's Solved these Questions
Similar Questions
Classify the following as rectilinear motion (motion along a straight line), circular motion or periodic motion (oscillatory motion) :
Motion of a horse pulling a cart on a straight road.
View SolutionClassify the following as motion along a straight line, circular oroscillatory motion:
Motion of your hands while running.
View Solution
Knowledge Check
A girl riding a bicycle along a straight road with a speed of 5 ms−1 throws a stone of mass 0.5 kg which has a speed of 15 ms−1 with respect to the ground along her direction of motion. The mass of the girl and bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown ? What is the change in speed, if so
A2.0ms−1B0.1ms−1C0.5ms−1D5.2ms−1In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision
 AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth l
AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth lIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QThe graph shows the psition of a hard ball with respect to time .The hard ball hits and rebounds on the hard surface .Ehich of the following graph represent the correct variation with repect to time?
 A
A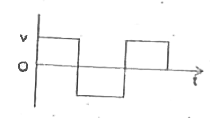 B
B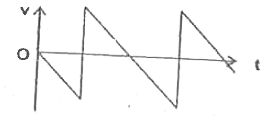 C
C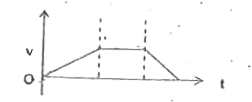 Dnone of these
Dnone of these
A girl ridding a bicycle along a straight road with a speed of 5ms−1 throws a stone of mass 0.5 kg which has a speed of 15ms−1 with respect to the ground along her direction of motion. The mass of the girl and bicycle is 5kg . Does the speed of the bicycle change after the stone is thrown ? What is the change in speed, if so ?
View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View SolutionClassify the following as motion along a straight line, circular oroscillatory motion: Motion of a Bus on a straight Road.
View Solution(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
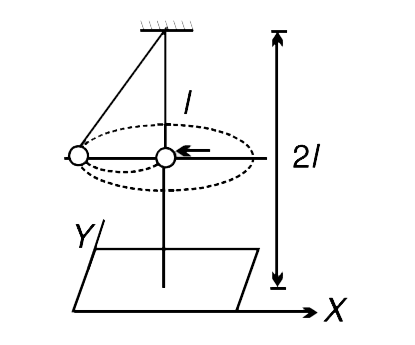
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
View SolutionClassify the following as motion along a straight line, circular oroscillatory motion:
Motion of a horse pulling a cart on a straight road.
View Solution
