Both neon [MNe=20×10−3kg] and helium [MHe=4×10−3kg] are monoatomic gases and can be assumed to be ideal gases. The fundamental frequency of a tube (open at both ends ) of neon is 300Hz at 270K(R=(25/3)J/Kmol)
The length of the tube is
512m
√312m
5√312m
(5√3)m
The correct Answer is:C
To find the length of the tube open at both ends for neon gas, we can use the formula for the fundamental frequency of a tube, which is given by:
f=12Lv
where:
- f is the fundamental frequency,
- L is the length of the tube,
- v is the velocity of sound in the gas.
The velocity of sound in an ideal gas can be calculated using the formula:
v=√γRTM
where:
- γ is the adiabatic index (ratio of specific heats),
- R is the universal gas constant,
- T is the absolute temperature,
- M is the molar mass of the gas.
Step 1: Identify the values
- For neon:
- f=300Hz
- T=270K
- R=253J/K mol
- M=20×10−3kg
- γ=53
Step 2: Calculate the velocity v
Using the formula for velocity:
v=√γRTM
Substituting the values:
v=
⎷53⋅253⋅27020×10−3
Step 3: Simplify the expression for v
Calculating the numerator:
53⋅253⋅270=5⋅25⋅2709=337509=3750
Now, substituting back into the velocity equation:
v=√375020×10−3=√37500.02=√187500=433.01m/s
Step 4: Calculate the length L
Now substituting v back into the fundamental frequency equation:
f=12Lv⟹L=v2f
Substituting the values:
L=433.012⋅300=433.01600≈0.72168m
Step 5: Final expression for length
To express the length in a simplified form, we can calculate:
L≈5⋅√312m
Conclusion
Thus, the length of the tube is approximately:
L≈0.72168m
- f is the fundamental frequency,
- L is the length of the tube,
- v is the velocity of sound in the gas.
- γ is the adiabatic index (ratio of specific heats),
- R is the universal gas constant,
- T is the absolute temperature,
- M is the molar mass of the gas.
- For neon:
- f=300Hz
- T=270K
- R=253J/K mol
- M=20×10−3kg
- γ=53
Using the formula for velocity:
⎷53⋅253⋅27020×10−3
Calculating the numerator:
Now substituting v back into the fundamental frequency equation:
To express the length in a simplified form, we can calculate:
Thus, the length of the tube is approximately:
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type
56 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Both neon [MNe=20×10−3kg] and helium [MHe=4×10−3kg] are monoatomic gases and can be assumed to be ideal gases. The fundamental frequency of a tube (open at both ends ) of neon is 300Hzat270K(R=(25/3)J/Kmol)
The fundamental frequency of the tube if the tube is filled with helium , all other factors remaining the same is
View SolutionA wire of radius 10−3m and length 2m is stretched by a force of 50 N. Calculate the fundamental frequency of the note emitted by it. Density of wire is 1.6.×103 kg m−3.
View SolutionA tube of a certain diameter and of length 48cm is open at both ends. Its fundamental frequency is found to be 320Hz. The velocity of sound in air is 320m/sec. Estimate the diameter of the tube.
View SolutionA glass plate of length 0.1m, breadth 15×103m and thickness 2×10−3m weighs 8×10−3kg in air, it is held vertically with its longer side horizontal and its lower half immersed in water. If the surfaces tension of water is 72×10−3N/m, the apparent weight of the plate is 79.4λ×10−3N. Then find λ
View SolutionThe length of a sonometer wire is 0.75 m and density is 9 × 103 kg/m3. It can bear a stress of 8.1 × 108 N/m2 without exceeding the elastic limit. Then the fundamental frequency that can be produced in the wire is
View SolutionA uniform rod of length 20 cm is clamped at the two points A and B as shown. Then the fundamental frequency of longitudinal vibration of the rod is (Y=2×1011N/m2,ρ=8×103kg/m3)

View SolutionLongitudinal waves of frequency 400Hz are produced in a rod of material of density 8000kg/m3 and Young modulus 7.2×1010N/m2. What is the wavelength of the wave?
View SolutionThe mass of an electron is 9.1×10−31kg. If its K.E. is 3.0×1025J. Calculate its wavelength .
View SolutionTwo kg of a monoatomic gas is at a pressure of 4×104N/m2. The density of the gas is 8kg/m3. What is the order of energy of the gas due to its thermal motion ?
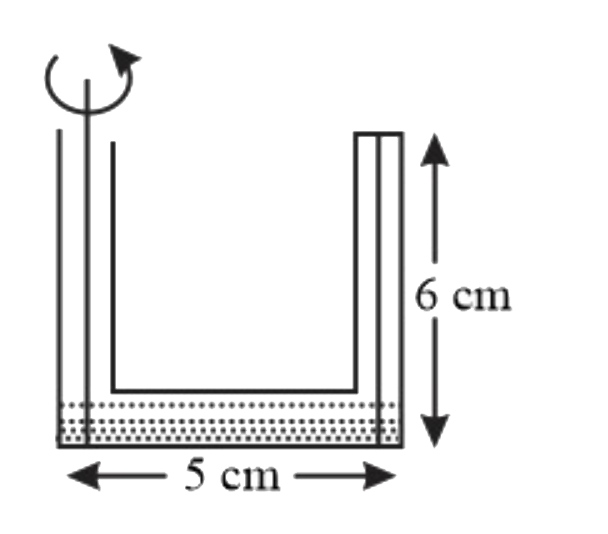
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View Solution
