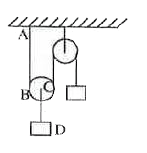
Both the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string AB is v1 and in CD it is v2, the v1/v2 is

If T1andT2 are the tensions in strings AB and CD resepctively then T2=2T1.
since v∝√T
we have v1v2=√T1T2
∴v1v2=1√2
Topper's Solved these Questions
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Theoretical questions :)
85 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Statement type questions:)
18 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
Similar Questions
both the strings , shown in figure are made of same material and have same cross - section. The pulleys are light the wave speed pf a travsverse wave in the string AB is v1 and in CD is v2. The ratio v1/v2 is

View SolutionIn the circuit shown in figure find Vab at 1s

View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vAvB is
View SolutionBoth the blocks shown in figure have same mass 'm'. All the pulley and strings are massiess.

View SolutionTwo strings of copper are stretched to the same tension. If their cross-section area are in the ratio 1 : 4 , then the respective wave velocities will be
View SolutionA string of length l is stretched by 1/30 and transverse waves in the string are found to travel at a speed v0. Speed of transverse waves when the string is stretched by 1/15 will be :
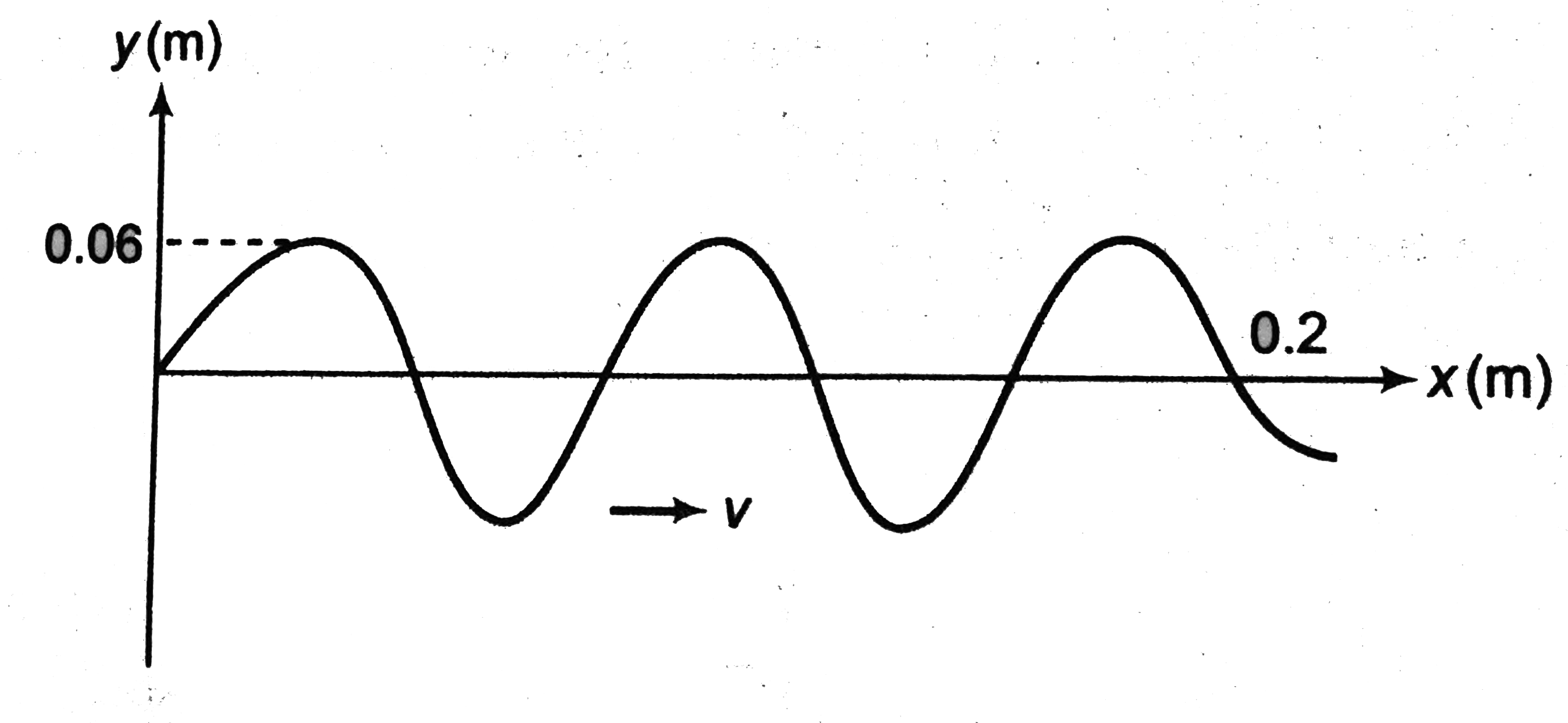
View SolutionFor the wave shown in figure, write the equation of this wave if its position is shown at t=0. Speed of wave is v=300m/s.
View SolutionTwo strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View Solution
