By sucking a straw a student can reduce the pressure in his lungs to 750mm of Hg(density)=13.6kg/cm3) Using the straw, he can drink water from a glass up to a maximum depth of :
10.2 cm
75.3 cm
13.6 cm
1.96 cm
The correct Answer is:C
To solve the problem, we need to find the maximum depth of water that a student can drink using a straw when he reduces the pressure in his lungs to 750 mm of Hg.
1. Understand the Pressure Difference:
When the student sucks on the straw, he creates a pressure difference between the atmospheric pressure and the pressure in his lungs. This pressure difference allows him to lift the water up the straw.
2. Pressure Calculation:
The pressure difference created by the reduction in lung pressure is given as:
ΔP=Patm−Plungs=Patm−750mm Hg
For simplicity, we can consider atmospheric pressure Patm to be 760 mm Hg.
3. Calculate the Pressure Difference:
The pressure difference can be calculated as:
ΔP=760mm Hg−750mm Hg=10mm Hg
4. Relate Pressure Difference to Fluid Height:
The pressure difference can also be expressed in terms of the height of the water column (h) that can be supported by this pressure difference:
ΔP=h⋅ρ⋅g
where ρ is the density of the fluid (water in this case) and g is the acceleration due to gravity.
5. Convert Density of Mercury to Density of Water:
The density of mercury is given as ρHg=13.6g/cm3 or 13600kg/m3. The density of water is ρwater=1000kg/m3.
6. Calculate Maximum Height of Water (h):
Using the relationship between the pressure difference and the height of the water column:
h=ΔP⋅ρHgρwater
Substituting the values:
h=10mm Hg⋅13.6g/cm31g/cm3
Since 1mm Hg corresponds to a height of 1.36cm of water, we can convert:
h=10⋅13.6=136cm
7. Final Result:
The maximum depth of water that the student can drink using the straw is:
h=136cm or 1.36m
When the student sucks on the straw, he creates a pressure difference between the atmospheric pressure and the pressure in his lungs. This pressure difference allows him to lift the water up the straw.
The pressure difference created by the reduction in lung pressure is given as:
ΔP=Patm−Plungs=Patm−750mm Hg
For simplicity, we can consider atmospheric pressure Patm to be 760 mm Hg.
The pressure difference can be calculated as:
ΔP=760mm Hg−750mm Hg=10mm Hg
The pressure difference can also be expressed in terms of the height of the water column (h) that can be supported by this pressure difference:
ΔP=h⋅ρ⋅g
where ρ is the density of the fluid (water in this case) and g is the acceleration due to gravity.
The density of mercury is given as ρHg=13.6g/cm3 or 13600kg/m3. The density of water is ρwater=1000kg/m3.
Using the relationship between the pressure difference and the height of the water column:
h=ΔP⋅ρHgρwater
Substituting the values:
h=10mm Hg⋅13.6g/cm31g/cm3
Since 1mm Hg corresponds to a height of 1.36cm of water, we can convert:
h=10⋅13.6=136cm
The maximum depth of water that the student can drink using the straw is:
h=136cm or 1.36m
Topper's Solved these Questions
Similar Questions
A capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as x1,x2 and x3 .

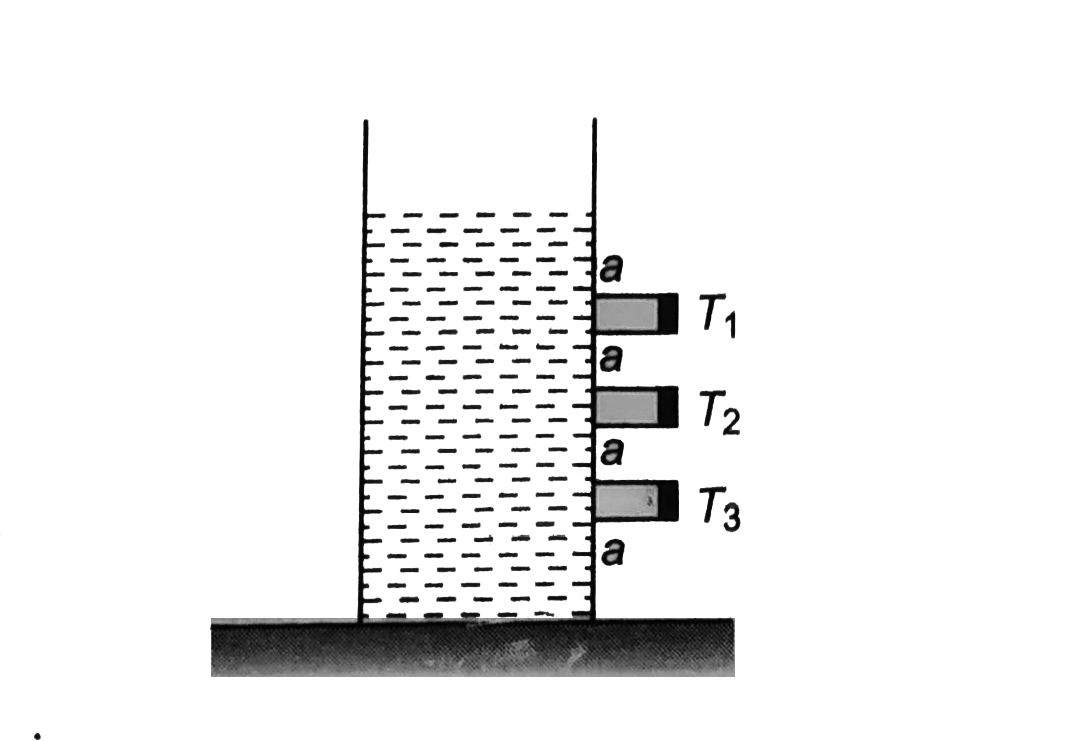
Distance x3 is given by
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as (x1),(x2) and (x3) .

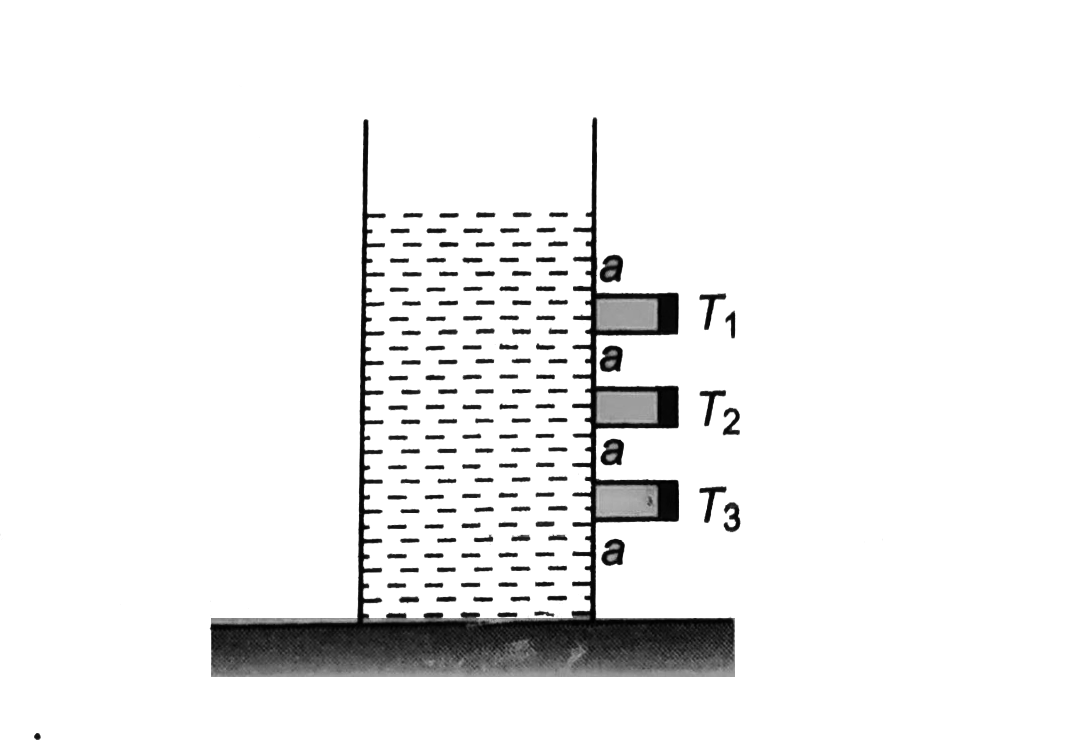
1. speed of efflux is
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes T1,T2 and T3 are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as x1,x2 and x3 .

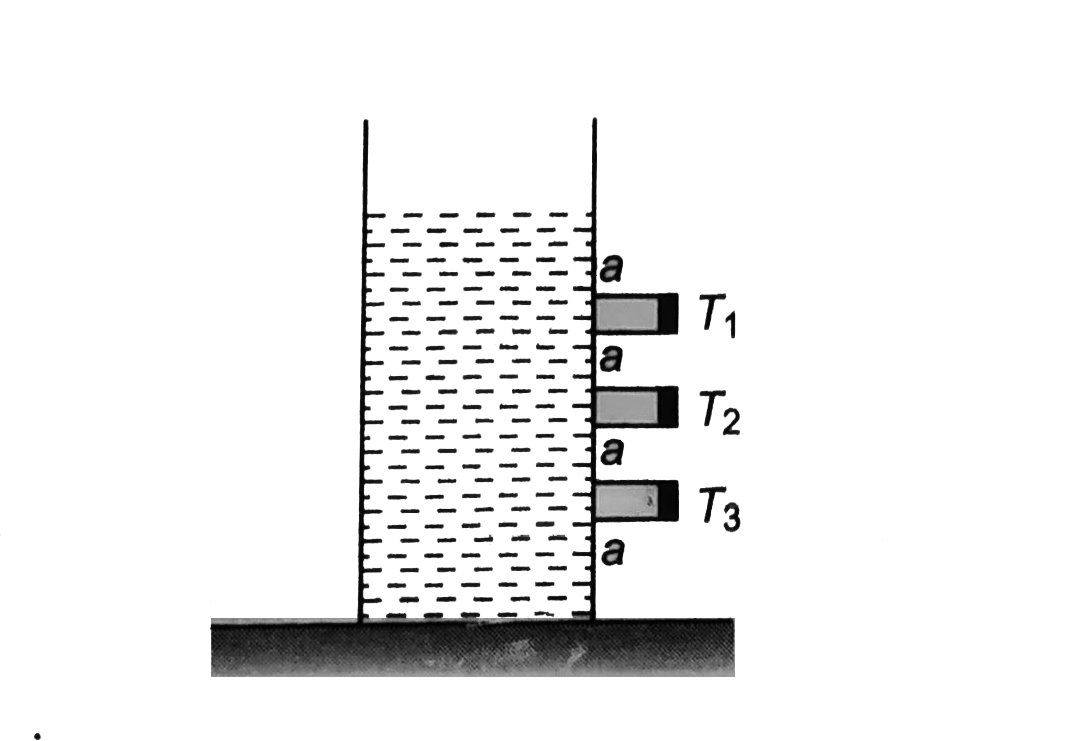
The correct sketch is
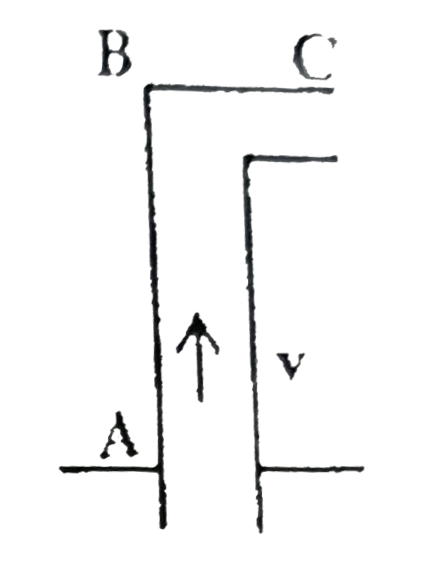
View SolutionABC is a light pipe lying in a vertical plane and of cross sectional area 1cm2 whose small part is in ground to fix the pipe. An ideal fluid of density 104kg/m3 is being flown through the pipe by means of external agency. Length of BC can be neglected. The minimum vertical upward force required to pull out the pipe from ground is F=9N. What should be maximum velocity (in m/s) of the fluid so that pipe can not be pulled out from ground ?
View SolutionA cylindrical tube with a frictionless piston ends in a small hole of area of cross–section 2×10−6m2, which is very small as compared to the area of cross-section of the tube. The tube is filled with a liquid of density 104kg/m3. The tube is held horizontal and the piston is pushed at a constant speed so that liquid comes out of the hole at a constant rate 'Q'm3/s. No liquid leaks around the piston. The material of the tube can bear a maximum pressure 6×105 Pa. The maximum possible value of Q so that the tube does not break is __________ ×10−5m3/s. [Atmospheric pressure =105 Pa]

View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. What is the viscous force on a glass sphere of radius r=1mm falling through water (η=1×10−3Pa−s) when the sphere has speed of 3m/s?
View SolutionAn air bubble rises the bottom of a lake to the top and increases thereby its volume 15 times . If the atmospheric pressure is 75 cm of hg and density of lake water is 1.02×103kg/m3 then find the depth of lake ( Neglect surface tension).
View SolutionIn the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of 2×10−3kg/m that passes over a light pulley . The string is connected to a vibrator of frequency 700Hz and the length of the string between the vibrator and the pulley is 1m.

The string is set into vibrations and represented by the equation y=6sin(πx10)cmcos(14×103πt) where x ane y are in cm , and t in s, the maximum displacement at x=5m from the vibrator is
View SolutionThe area of base of a cylindrical vessel is 300cm2. Water (density=1000kgm−3) is poured into it up to a depth of 6 cm. Calculate : (a) the pressure and (b) the thrust of water on the base. (g=10ms−2).
View Solution
