Calculate de-Broglie wavelength of hydrogen molecules (H2) present in a container at 400K. Assume that molecules travel at rms speed. Boltzmann constant k=1.38×10–23JK–1 Mass of H2 molecule =2.0aμ
The correct Answer is:1.02Å
Step by step video, text & image solution for Calculate de-Broglie wavelength of hydrogen molecules (H_(2)) present in a container at 400 K. Assume that molecules travel at rms speed. Boltzmann constant k = 1.38 × 10^(– 23) JK^(– 1) Mass of H_(2) molecule = 2.0 amu by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
In the figure shown M represents a mirror. AB is an incident wavefront. Which type of mirror is M if the reflected wave front
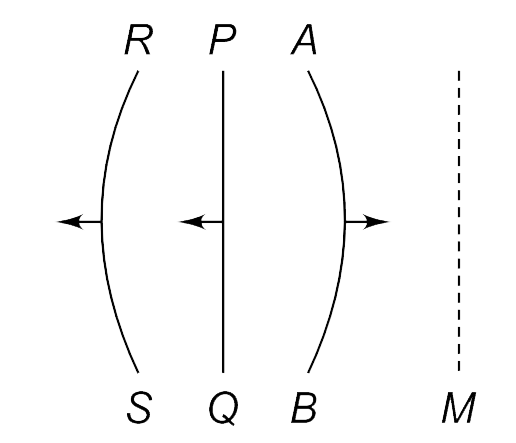
(a)PQ (b)RS02:18View SolutionThe diameter of a gas molecule is 2.4×10−10m. Calculate the mean free path at NTP. Given Boltzmann constant k=1.38×10−23Jmo≤ce–−1K−1.
04:39View SolutionWhat is the de-Broglie wavelength of nitrogen molecule in air at 300K ? Assume that the molecule is moving with the root mean square speed fo molecules at this temperature. (Atomic mass of nitrogen =14.0076U) Plank's constant=6.63×10−34Js , Boltzmann constant =1.38×10−23JK−1
01:28View SolutionThe de Broglie wavelength of a molecules of thermal energy KT ( K is Boltzmann constant and T is absolute temperture) is given by
02:36View SolutionCalculate the average momentum of a hydrogen molecule at 20^(@)C . Boltzmann constant =1.38xx10^(-23) JK^(-1) and mass of a hydrogen molecule =3.2xx10^(-27)kg .
03:36View Solution0∘C पर किसी गैस के अणु की औसत गतिज ऊर्जा ज्ञात करो | यदि बोल्ट्जमैन स्थिरांक k=1.38×10−23 जूल/अणु K | क्या यह गैसीय अणु की प्रकृति पर भी निर्भर है |
03:16View SolutionWhat is the de Broglie wavelength of anitrogen molecule at 300 K? Assume the molecule to be moving with its rms speed. [Atomic mass of nitrogen = 14.0076 u ]
03:36View SolutionCalculate the kinetic energy per molecule and also rms velocity of a gas at 127∘C .
Given kB=1.38×10−23Jmolecule−1K−1 and mass per molecule of the gas =6.4×10−27 kg .03:36View SolutionCalculate the kinetic energy per molecule and also rms velocity of a gas at 127^@C . Given k_B = 1.38 xx10^(-23) J "molecule"^(-1) K^(-1) and mass per molecule of the gas =6.4xx10^(-27) kg .
01:58View SolutionAssuming the nitrogen molecule is moving with r.m.s. velocity at 400K, the de Broglie wavelength of nitrogen molecule is close to : (Given : nitrogen molecule weight : 4.64 xx 10^(-26) kg, BoItzman constant : 1.38 xx 10^(-23) j//K , Planck constant : 6.63 xx 10^(-34)J.s )
02:50View SolutionNitrogen gas is at 300∘C temperature . The temperature ( in K) at which the rms speed of a H2 molecule would be equal to the rms speed of a nitrogen molecule is ,_________ .
03:53View SolutionAt a temperature of 314 K and a pressure of 100 kPa , the speed of sound in a gas is 1380 ms^(-1) . The radius of each gas molecule is 0.5 Å . The frequency of sound at which the wavelength of sound wave in the gas becomes equal to the mean free path of the gas molecules is ( Boltzmann constant = 1.38 xx 10^(-23) JK^(-1) . )
04:50View SolutionA diamtomic gas consisting of rigid molecules is at a temperature of 87^(@)C . If the moment of inertia is 2.76 xx 10^(-39) gcm^(2) , then the rms angular speed of the molecule is (Boltzmann constant = 1.38 xx 10^(-23)JK^(-1) )
06:04View SolutionWhat is the de-Broglie wavelength of nitrogen molecule in air at 300K ? Assume that the molecule is moving with the root mean square speed of molecules at this temperature. (Atomic mass of nitrogen =14.0076U) Plank's constant=6.63×10−34Js , Boltzmann constant =1.38×10−23JK−1
02:13View SolutionAssuming the nitrogen molecule is moving with r.m.s. velocity at 400K, the de Broglie wavelength of nitrogen molecule is close to :
(Given : nitrogen molecule weight : 4.64×10−26kg, BoItzman constant : 1.38×10−23j/K, Planck constant : 6.63×10−34J.s)03:06View Solution

