Calculate the angle of (a) 1∘ (degree) (b) 1' (minute of arc of are min) and (c ) 1''(secondof arc of arc sec) in radian. Use 360∘=2πrad.,1∘=60' and 1' = 60''.
Video Solution
Text Solution
(a) We have 360∘=2πrad
1∘=(π/180)rad=1.745×10−2rad
(b) 1∘=60'=1.745×10−2rad
1'=2.908×10−4rad≅2.91×10−4rad
(c) 1'=60''=2.908×10−4rad
1''=4.847×10−4rad≅4.85×10−6rad
|
Topper's Solved these Questions
- UNITS AND MEASUREMENTBook:NCERTChapter:UNITS AND MEASUREMENTExercise:EXERCISE
Explore 33 Videos
- UNITS AND MEASUREMENTBook:NCERTChapter:UNITS AND MEASUREMENTExercise:QUESTION
Explore 1 Video
- THERMODYNAMICSBook:NCERTChapter:THERMODYNAMICSExercise:EXERCISE
Explore 10 Videos
- WAVESBook:NCERTChapter:WAVESExercise:EXERCISE
Explore 27 Videos
Similar Questions
Knowledge Check
Calulate the angle of 1" (secondof arc or arc sec) in radian. (Use 360∘=2π rad, 1∘=60'and1'=60")
A4.85×10−6radB4.85×106radC4.85×105radD4.85×10−5radThe angle of 1' (minute of arc) in radian is nearly equal to
A2.91x10−4radB4.85x10−4radC4.80x10−6radD1.75x10−2radThe angle of 1' (minute of arc) in radian is nearly equal to
A4.85×10−4radB4.80×10−6radC1.75×10−2radD2.91×10−4rad
Find the value of : arcsin(12)+arccos(12)
View Solution∫arcsinxdx√1+x.
View SolutionCompute the integrals :
∫10xarctanxdx
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
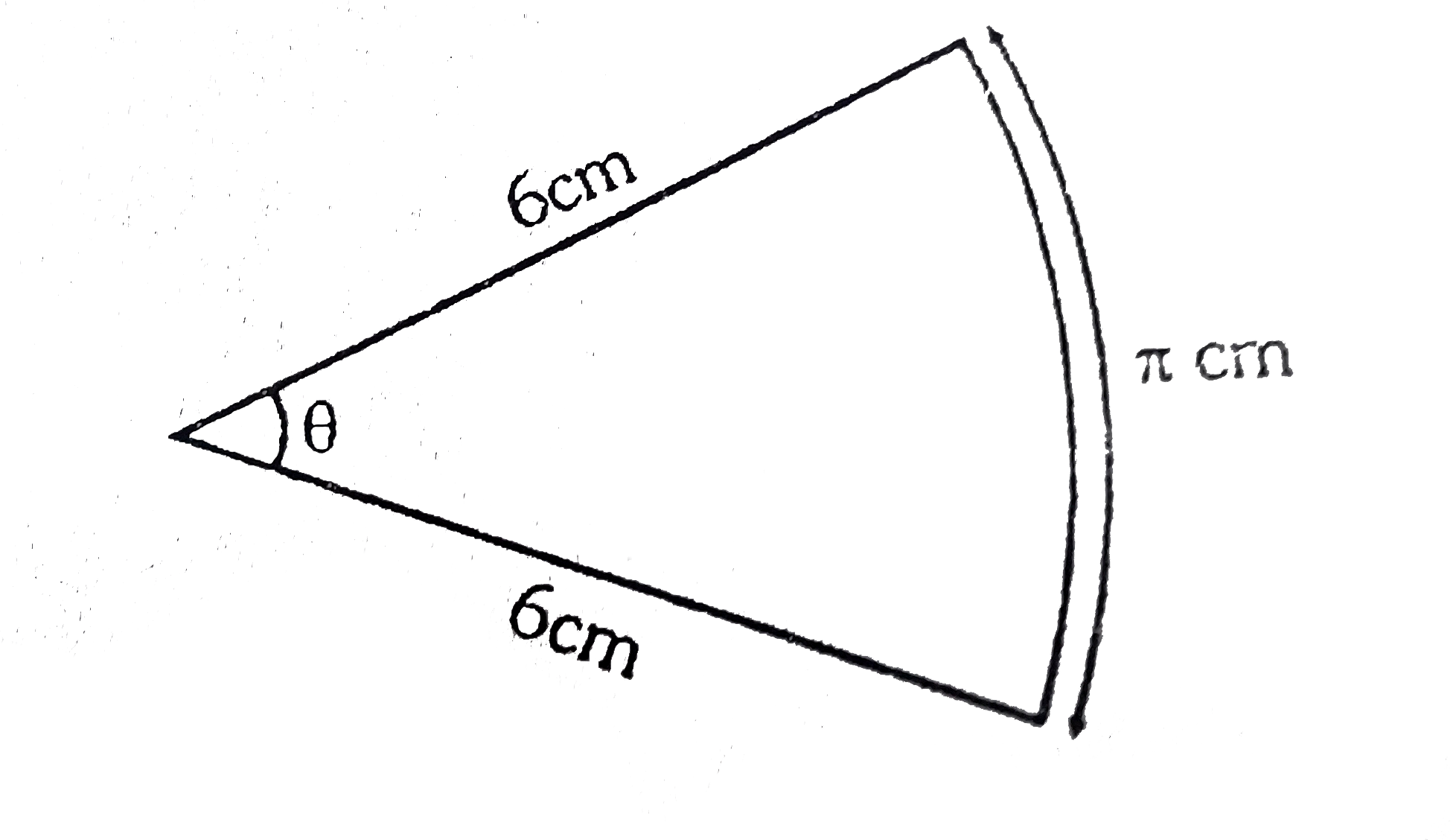
View SolutionAn arc subtended an angle 60∘ at the center of c circle of radius 6 cm , then length of minor and major arc
View Solution