Calculate the angle of
(i) 1∘ (degree)
(ii) 1∘ (minute of arc or arc minute) and
(iii) 1∘ (second of arc or arc sec)
in radian.(Use 360∘=2πrad,1∘=60∘ and 1′=60∘ and 1′=60'')
Video Solution
Text Solution
(I) 1∘−2π360rad=π180rad=227×180rad=1.746×10−2rad
(ii) 1 arc min = 1′=1∘60=160×π180rad=2.91×10−4rad
(iii) 1 arc sec= 1′1∘60=1∘60×60=160×60×π180=rad
4.85×10−6rad
|
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.1
25 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.2
10 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEYCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
Similar Questions
Knowledge Check
Calulate the angle of 1" (secondof arc or arc sec) in radian. (Use 360∘=2π rad, 1∘=60'and1'=60")
A4.85×10−6radB4.85×106radC4.85×105radD4.85×10−5radThe angle of 1' (minute of arc) in radian is nearly equal to
A2.91x10−4radB4.85x10−4radC4.80x10−6radD1.75x10−2radThe angle of 1' (minute of arc) in radian is nearly equal to
A4.85×10−4radB4.80×10−6radC1.75×10−2radD2.91×10−4rad
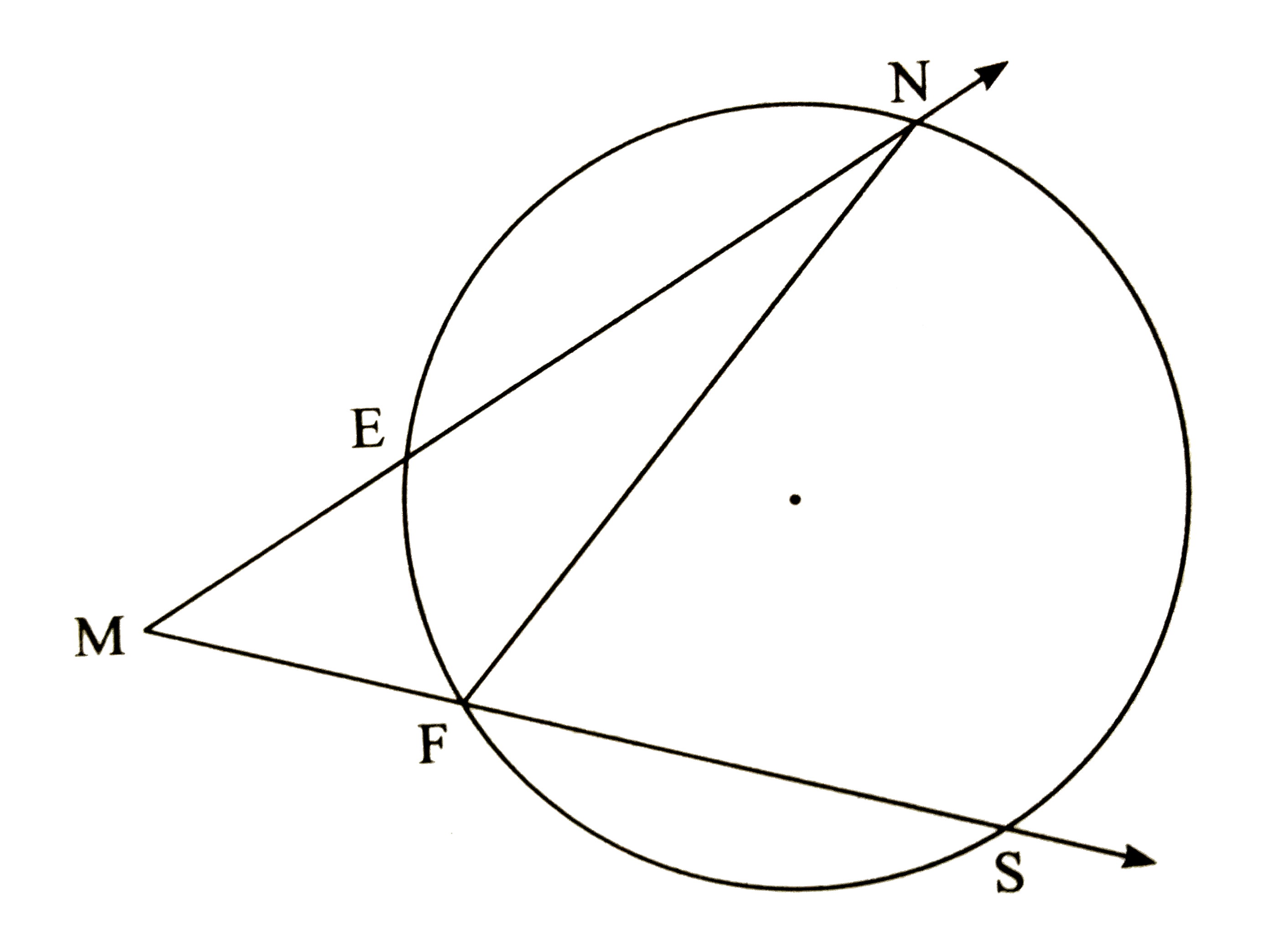
In the figure, m ( arc NS ) =130∘
m (arc EF ) =60∘. Find
(i) ∠NMS
(ii) ∠ENF
( iii) ∠NFS
View SolutionFind the value of sin[arccos(−12)]
View SolutionFind the length of the arc of a sector of a circle with radius 6 cm whose angle is 60∘.
View SolutionCompute the integrals :
∫10 arc tan √xdx
View SolutionIf central angle of an arc is 60∘ then the ratio of areas of minor sector and major sector will be
View Solution
