Calculate the angle θ subtended by the two adjacent wooden spokes of a bullock cart wheel is shown in the figure. Express the angle in both radian and degree.

The full wheel subtends 2π radians at the center of the wheel. The wheel is divided into 12 parts arcs).
So one part subtends an angle θ=2π12=π6 radian at the center
Since, π rad =180∘,π6 radian is equal to 30 degree.
∴ The angle subtended by two adjacent wooden spokes is 30 degree at the center.
Topper's Solved these Questions
- KINEMATICSBOOK - FULL MARKSCHAPTER - KINEMATICSEXERCISE - TEXTUAL QUESTIONS SOLVED (MULTIPLE CHOICE QUESTIONS:)
30 Videos
- KINEMATICSBOOK - FULL MARKSCHAPTER - KINEMATICSEXERCISE - TEXTUAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS)
30 Videos
- HEAT AND THERMODYNAMICSBOOK - FULL MARKSCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - ADDITIONAL QUESTIONS SOLVED (Numerical Problems)
16 Videos
- KINETIC THEORY OF GASESBOOK - FULL MARKSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Addtional Numerical Problems
10 Videos
Similar Questions
Knowledge Check
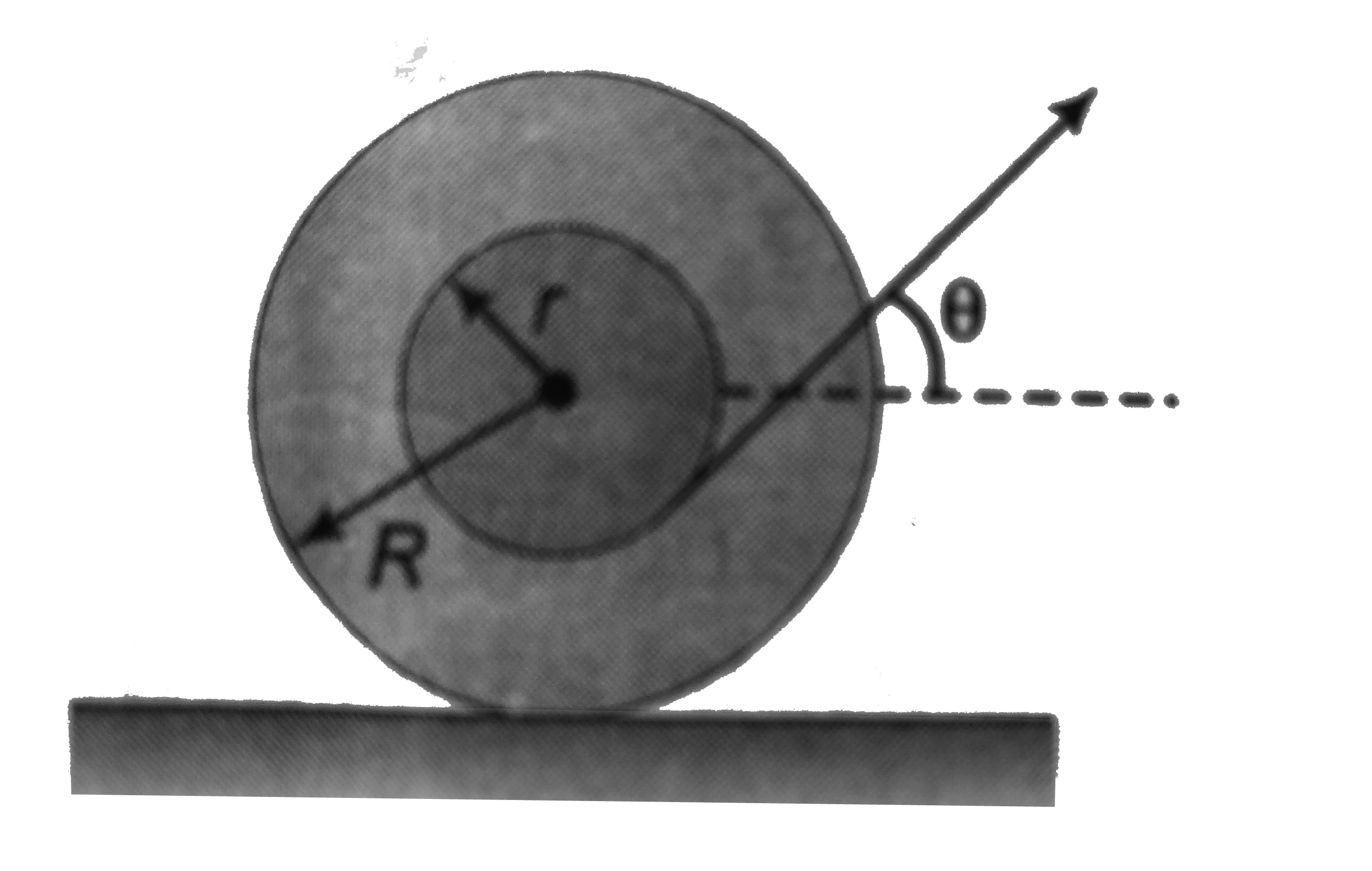
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal toAcos−1(Rr)Bsin−1(√1−r2R2)Cπ−cos−1(rR)Dsin−1(rR)
The difference between the two acute angles of a right angled triangle is 2π5 radians. Express the angles in degrees.
View SolutionIf a bicycle wheel has 48 spokes, then find the angle between a pair of adjacent spokes.
View SolutionThe difference between the two acute angles of a right angled triangle is π9 radians. Express the angles in degrees.
View Solution
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View SolutionIf a bicycle wheel has 48 spokes, then find the angle between a pair of adjacent spokes.
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
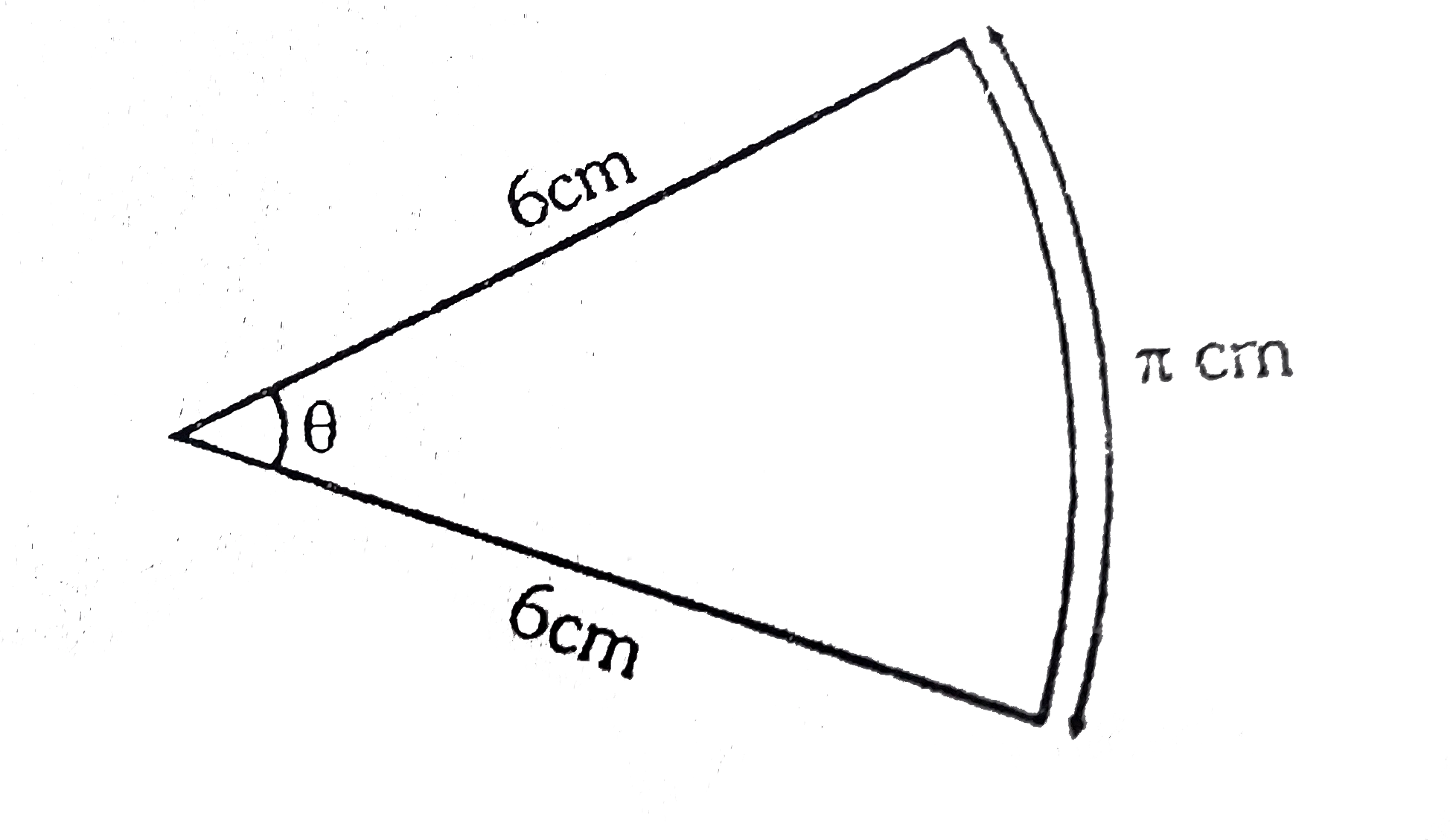
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.

View Solution

