Calculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass $M$ and radius $R$ . (Assume the base of hemisphere to be open)

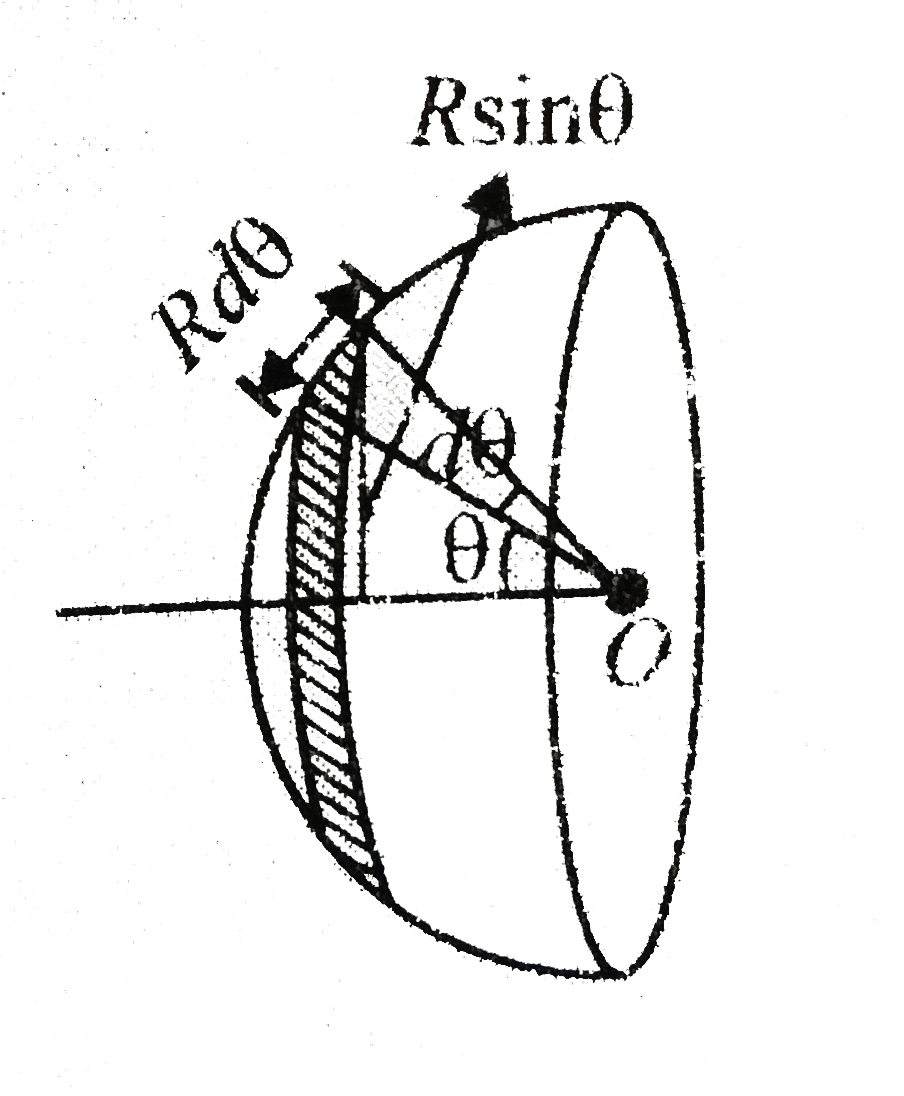
Video Solution

Text Solution

Verified by Experts

We consider the shaded elemental ring of mass
$d m = \frac{M}{(2 π R^{2})} 2 π R sin θ (R d θ)$
Field due to this ring at $O$
$d E = \frac{G d m R cos θ}{R^{3}}$
(see formulae for field due to a ring)
or $d E = \frac{G M}{R^{2}} sin θ cos θ d θ$
Hence $E = \int_{0}^{π / 2} d E = \int_{R^{2}}^{π / 2} \frac{G M}{R^{2}} sin θ cos θ d θ$
or $E = \frac{G M}{2 R^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the moment of inertia of a hemisphere of mass $M$ and radius $R$ shown in the figure, about an axis $A A'$ tangential to the hemisphere.

A $I = (\frac{9}{20}) m R^{2}$
B $I = (\frac{13}{20}) m R^{2}$
C $I = (\frac{7}{20}) m R^{2}$
D $I = (\frac{3}{20}) m R^{2}$
Question 2 - Select One
If the total suface area of a hemisphere is 27 $π$ square cm, then the radius of the base of the hemisphere is
A $9 \sqrt{3}$ cm
B3 cm
C $3 \sqrt{3}$
D9 cm
Question 3 - Select One
Find distance of centre of mass of solid hemisphere of radius 8cm from centre
A3 cm
B3/8 cm
C4 cm
D2 cm

CENGAGE PHYSICS-GRAVITATION-INTEGER_TYPE

Home
Ask Doubt
Profile