Calculate the number of moles of air is in the inflated ballon at room temperature as shown in the figure

The radius of the ballon is 10 cm and pressure inside the balloon is 180 k Pa.
The radius of the balloon R=10×10−2m
The pressure inside the balloon P=1.8×105P
Room temperature
T=303k(273+30)
Number of moles of air μ=?
μ=vPRT
V- volume of air in balloon V=43μR3
∴,μ=43×3.14×(10×10−2)3×1.8×1058.314×303 ,
μ=0.3 moles
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SURA PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - Additional Questions ( Multiple Choice Qustion )
44 Videos
- HEAT AND THERMODYNAMICSBOOK - SURA PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - (II) Match the Following
1 Videos
- HEAT AND THERMODYNAMICSBOOK - SURA PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - III Long Answer Questions:
24 Videos
- GRAVITATIONBOOK - SURA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - VALUE BASED QUESTIONS
4 Videos
- KINEMATICSBOOK - SURA PUBLICATIONCHAPTER - KINEMATICSEXERCISE - Creative Question (HOTS)
12 Videos
Similar Questions
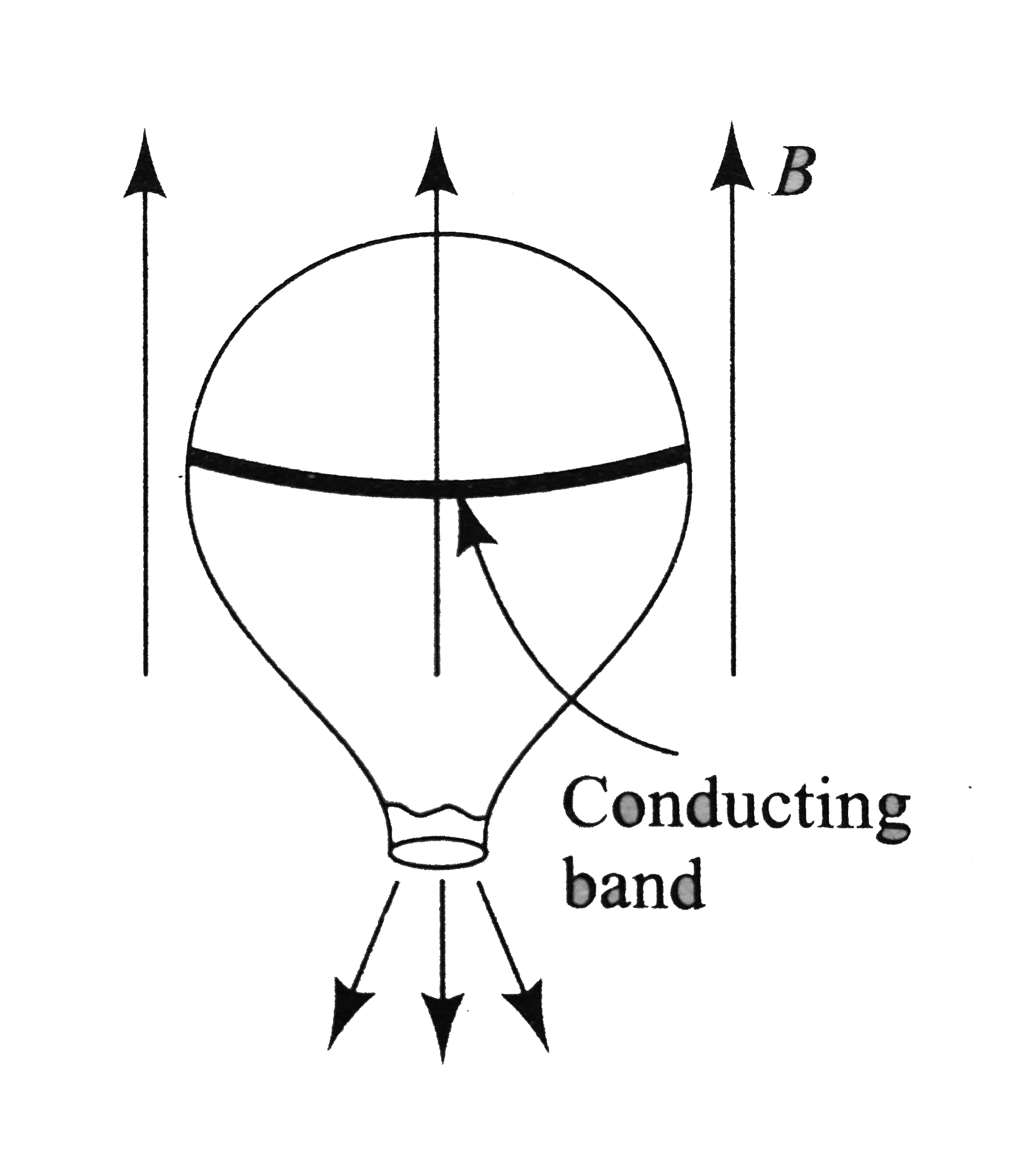
An elasticized conducting band is around a spherical ballon . Its plane through the center of the balloon. A uniform nmagnetic field of magnitude 0.04T is directed perpendicular to the plane of the band. Air is let out of the balloon at 100cm3s−1 at an instant when the radius of the balloon is 10cm. The induced emf in the band is
View SolutionSuppose there is an air bubble of radius inside the air cavity of radius R inside a water drop of radius 3R as shown in figure. The ratio of gauge pressure at point C to gauge pressure at point B is: -B
View Solution
Knowledge Check
An elasticized conducting band is around a spherical ballon . Its plane through the center of the balloon. A uniform nmagnetic field of magnitude 0.04T is directed perpendicular to the plane of the band. Air is let out of the balloon at 100cm3s−1 at an instant when the radius of the balloon is 10cm. The induced emf in the band is
 A(a) 15μvB(b) 25μvC( c) 10μvD(d) 20μv
A(a) 15μvB(b) 25μvC( c) 10μvD(d) 20μvThe radius of a spherical balloon increases from 6 cm to 10 cm when more air is pumped into it. The ratio in the surface area of the original balloon and the inflated balloon is:
A4:5B27:125C3:5D9:25A balloon containing 1 mole air at 1 atm initially is filled further with air till pressure increases to 4 atm. The intial diameter of the ballon is 1 m and the pressure at each stage is proportional to diameter of the balloon. How many moles of air added to change the pressure from 1 atm to 4 atm.
A80B257C255D256
Suppose there is an air bubble of radius inside the air cavity of radius R inside a water drop of radius 3R as shown in figure. The ratio of gauge pressure at point C to gauge pressure at point B is:
View SolutionA balloon containing 1 mole air at 1 atm initially is filled further with air till pressure increases to 3 atm. The intial diameter of the balloon is 1 m and the pressure at each state is proportion to diameter of the balloon. Calculate
( a) No. of moles of air added to change the pressure from 1 atm to 3 atm.
( b) balloon will burst if either pressure increases to 7 atm or volume increases to 36πm3.Calculate the number of moles of air that must be added after initial condition to burst the balloon.
View SolutionA ballon blown up with 1 mole of gas has a volume of 480mL at 5∘C The balloon is filled to (7/8) th of its maximum capacity Suggest
(a) Will the balloon burst at 30∘C
(b) The minimum temperature at which it will burst
(c ) The pressure of gas inside the balloon at 5∘C
(d) The pressure of gas when balloon bursts .
View SolutionAn air bubble has a radius of 0.50 cm at the bottom of a water tank where the temperature is 280 K and the pressure is 280 kPa. When the bubble rises to the surface, the temperature changes to 300 K and pressure to 300 K and pressure to 100 kPa. Calculate the radius of the bubble at the surface
View SolutionAn air bubble has a radius of 0.50 cm at the bottom of a water tank where the temperature is 280 K and the pressure is 280 kPa. When the bubble rises to the surface, the temperature changes to 300 K and pressure to 300 K and pressure to 100 kPa. Calculate the radius of the bubble at the surface
View Solution
