Calculate the velocity head of water which is flowing with a velocity of 5 m/s in a horizontal pipe.
To calculate the velocity head of water flowing in a horizontal pipe, we can follow these steps:
Step 1: Understand the concept of velocity head
The velocity head (h) is a measure of the kinetic energy of the fluid due to its velocity. It is given by the formula:
h=v22g
where:
- v is the velocity of the fluid (in m/s)
- g is the acceleration due to gravity (approximately 9.81m/s2)
Step 2: Identify the given values
From the problem, we know:
- The velocity v=5m/s
- The acceleration due to gravity g≈10m/s2 (for simplicity in calculations)
Step 3: Substitute the values into the formula
Now, we can substitute the values into the velocity head formula:
h=(5m/s)22×10m/s2
Step 4: Calculate the numerator
Calculate (5m/s)2:
(5m/s)2=25m2/s2
Step 5: Calculate the denominator
Calculate 2×10m/s2:
2×10m/s2=20m/s2
Step 6: Calculate the velocity head
Now substitute these values back into the equation:
h=25m2/s220m/s2
Perform the division:
h=1.25m
Final Answer
The velocity head of water flowing with a velocity of 5 m/s in a horizontal pipe is:
h=1.25m
---
The velocity head (h) is a measure of the kinetic energy of the fluid due to its velocity. It is given by the formula:
h=v22g
where:
- v is the velocity of the fluid (in m/s)
- g is the acceleration due to gravity (approximately 9.81m/s2)
From the problem, we know:
- The velocity v=5m/s
- The acceleration due to gravity g≈10m/s2 (for simplicity in calculations)
Now, we can substitute the values into the velocity head formula:
h=(5m/s)22×10m/s2
Calculate (5m/s)2:
(5m/s)2=25m2/s2
Calculate 2×10m/s2:
2×10m/s2=20m/s2
Now substitute these values back into the equation:
h=25m2/s220m/s2
Perform the division:
h=1.25m
The velocity head of water flowing with a velocity of 5 m/s in a horizontal pipe is:
h=1.25m
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Problems
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Water is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View Solution48.A block of mass 5kg is at rest on a smooth horizontal surface Water coming out of a pipe horizontally at the rate of 2kg/sec ,hits the block with a velocity of 6m/sec.The initial acceleration of the block is
View Solution
Knowledge Check
A pipe 2 cm in diameter has a constriction of diameter 1 cm. What it’s the velocity of flow at the constriction. If velocity of flow in the broader region of the pipe is 5 cm/s?
A10 cm/sB20 cm/sC25 cm/sD30 cm/sTwo horizontal pipes of radii 1 cm and 2cm are connected with one-another. Water is flowing through them. If the velocity of water in first pipe is 8ms−1 and the pressure is 1.0×105Nm−2, then pressure (in N m−2) and velocity (in ms−1) of water in second pipe are (Density of water =103kgm−3)
A1.0×105,8B2×105,16C1.3×105,2D1.8×105,4A storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
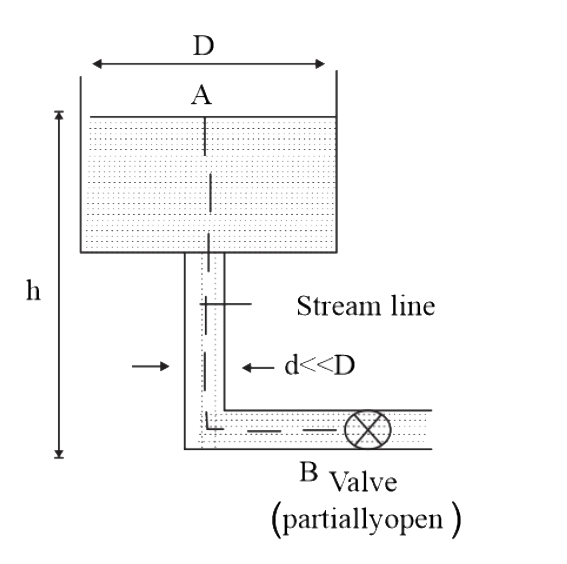 AP0BP0+ρghCP0+ρgh+12ρv2DP0+ρgh−12ρv2
AP0BP0+ρghCP0+ρgh+12ρv2DP0+ρgh−12ρv2
The rate of flow of water through a horizontal pipe of changing cross section is 100 litres per hour. Calculate the velocity of water flow at a point where diameter of the tube is 4 cm?
View SolutionTwo horizontal pipes of diameter 4 cm and 8 cm are connected together and water is flowing through the first pipe with a speed of 5 ms−1. Calculate the speed and pressure of water in the second pipe if water pressure in the first pipe is 3×104N/m2.
View SolutionAn engine pumps water through a hose pipe. Water passes, through the pipe and leaves it with a velocity of 2 m/s. The mass per unit length of water in the pipe is 100 kg//m. What is the power of the engine ?
View SolutionThe velocity of a boat in still water is 10m/s.If water flows in the river with a velocity of 6m/s what is the difference in times taken to cross the river in the shortest path and the shortest time.The width of the river is 80m.
View SolutionWater enters a horizontal pipe of non uniform cross section with a velocity of 0.5 m/s and leaves the other end with a velocity of 0.7 m/s. the pressure of water at the first end is 103N/m2. Calculate pressure at the other end. (Density of water =1.0×103kg/m3)
View Solution
