Can charge lie on a Gaussian surface?
Text Solution
Charge cannot lie on a Gaussian surface.
|
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Additional Question)
14 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Fill in the Blanks )
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Higher Order Thinking Skills & Advanced Level (Questions With Answers)
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
If net charge enclosed by a Gaussian surface is zero, then
Assertion :- →E at any point on Gaussian surface is 0.
Reason :- No net charge is enclosed by Gaussian surface, so E = 0AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False.Refer to the arrangement of charges in Fig and a Gaussian surface of radius R with Q at the centre. Then
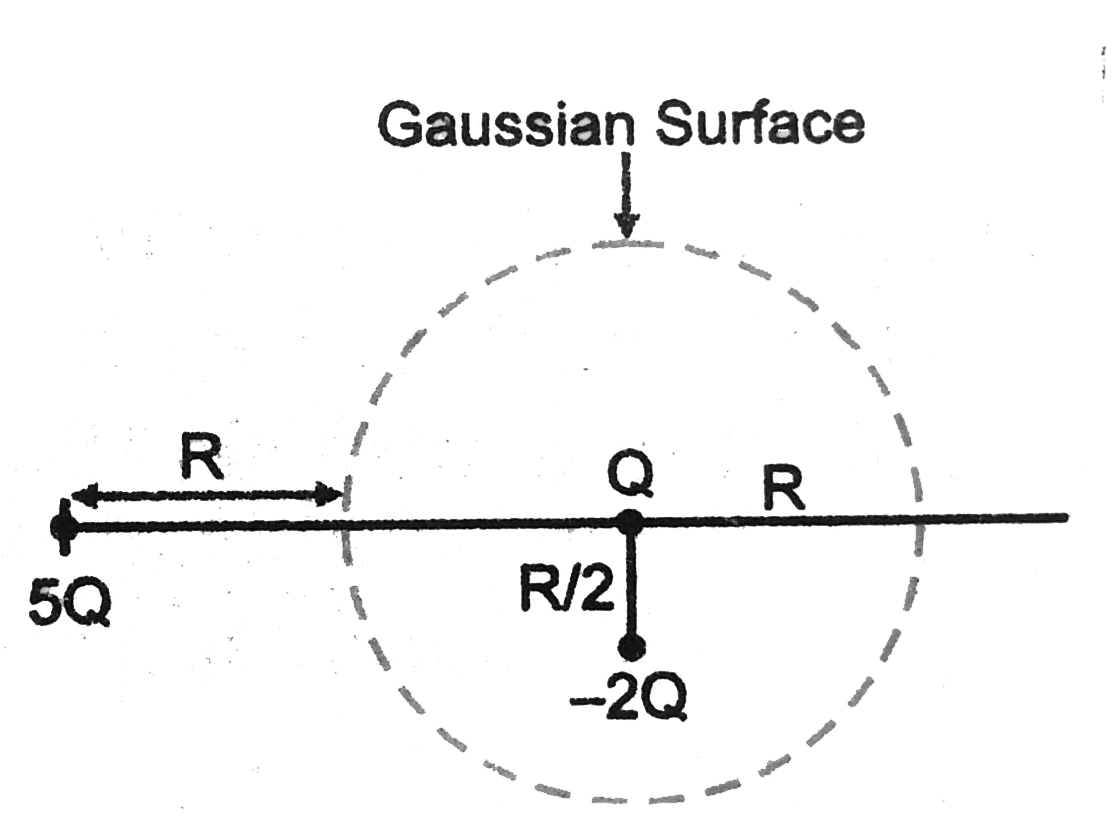 Atotal flux through the surface of the sphere is −Q∈0Bfield on the surface of the sphere si −Q4π∈0R2Cflux through the surface of sphere due to 5Q is zero.Dfield on the surface of sphere due to −2Q is same everywhere
Atotal flux through the surface of the sphere is −Q∈0Bfield on the surface of the sphere si −Q4π∈0R2Cflux through the surface of sphere due to 5Q is zero.Dfield on the surface of sphere due to −2Q is same everywhereA+q1 charge is at centre of an imaginary spherical Gaussion surface 'S', and −q1 charge is placed nearby this +q1 charge inside 'S'. A charge +q2 is located outside this Gaussian surface. Then electric field on Gaussian surface will be :
Adue to −q1 & q1BuniformCdue to all chargesDzero
Slection Of Gaussian Surface
View SolutionCan Gauss's law in electrostatics tell us exactly where the charge is located within the Gaussian surface ?
View SolutionAssertion(A):If Gaussian surface does not enclose any charge then →E at any point on the Gaussian surface must be zero.
Assertion(R ):No net charge is enclosed by Gaussians surface,so net flux passing through the surface is zero.
View SolutionA charge q is enclosed by an imaginary Gaussian surface.

If radius of surface is increasing at a rate drdt=K, then
View SolutionA point charge 4μC is at the centre of a cubic Gaussian surface 10 cm on edge. Net electric flux through the surface is
View Solution
