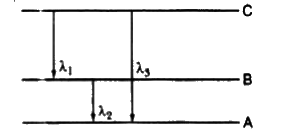
Certain substance emits only the wavelengths λ1,λ2,λ3 and λ4 when it is at a high temperature, it will absorb only the following wavelengths
λ1
λ2
λ1 and λ2
λ1,λ2,λ3 and λ4
The correct Answer is:D
If a body emits wavelength λ1,λ2,λ3 and λ4 at a high temperature then at a lower temperature it will absorb the radiation of same wavelength. This is accordance with Kirchhoff's law
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
The de-Broglie wavelength λ
Ais proportional to massBis proportional to impulseCInversely proportional to impulseDdoes not depend on impulseMomentum of a photon of wavelength λ is
AhλBZeroChλc2DhλcIn Young's double slit experiment, the 10th maximum of wavelength λ1 is at a distance y1 from its central maximum and the 5th maximum of wavelength λ2 is at a distance y2 from its central maximum. The ratio y1/y2 will be
A2λ1λ2B2λ2λ1Cλ12λ2Dλ12λ1
The wavelength λe of ann electron and λp of a photon of same energy E are related by
View SolutionNeglecting the mass variation with velocity , the ratio of the wavelength (λeλp) associated with an electron (λe) having a kinetic energy E and wavelength associated with a Photon (λp) having kinetie energy 4E is
View SolutionWhen a metallic surface of threshold wavelength 4λ is illuminated with light of wavelength λ the stopping potential is V. When the same surface is illuminated by the light of wavelength 2λ Stopping potential is V3 Threshold wavelength for the metallic surface is
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View SolutionIn a biprism experiment, if the 6th bright bannd with a wavelength λ1 coincides with 7th dark band with a wavelength λ2, then the ratio of the wavelengths (λ1λ2) is
View Solution