Charge on the outer sphere is q, and the inner sphere is grounded. Then the charge q' on the inner sphere is q', for
(r2>r1)

zero
q'=q
q'=−r1r2q
q'=r1r2q
The correct Answer is:C
Potential at the surface of inner sphere =0 (grounded)
14πε0qr2+14πε0q'r1=0
⇒q'=−qr1r2
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section B - Assertion Reasoning
17 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIPMTNEET Questions
38 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits
52 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
There are two concentric metal shells of radii r1 and r2(>r1). If initially, the outer shell has a charge q and the inner shell is having zero charge and then inner shell is grounded. Find :
(i) Charge on the inner surface of outer shell.
(ii) Final charges on each sphere.
(iii) Charge flown through wire in the ground.
View SolutionA spherical capacitor has an outer sphere of radius 0.15m and the inner sphere of diameter 0.2m The outer sphere is earthed and the inner shere is given charge of 6μC. The space between the concentric spheres is filled with a material of dielectric constant 6. Calculate capacitacne and potential of inner sphere.
View Solution
Knowledge Check
Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A−r2r1qBzeroC−r1r2qD−qCapcity of a spherical capacitor is C1 when in sphere is charged and outer sphere is earthed and when inner sphere is earthed and outer sphere charged. Then C1C2 is (a = radius of inner sphere b = radius of outer sphere)
A1BabCbaDa+ba−bA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
A54e.s.u.B14e.s.u.C30e.s.u.D36e.s.u.
A sphere of radius 10 cm conecentrically surrounded by a thin spherical shell of radius of 11 cm A charge of 100μC is imparted to the outer spheree and the inner one is earthed. Calculate the charge on the outer surface of the inner sphere and on the two surfaes of the outer sphere.
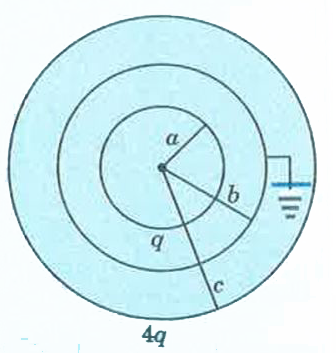
View SolutionThere are three concentric metallic spherical shells of radius a, b and c respectively as shown in the figure. The innermost sphere is given a charge q and the outermost sphere is given a charge 4q while the middle sphere is earthed. Find the charges appearing on the inner and outer surfaces of middle sphere.
View SolutionConsider two concentric conducting spheres. The outer sphere is hollow and initially has a charge −7Q on it. The inner sphere is solid and has a charge +2Q on it.
a. How much charge is on the outer surface and inner surface of the outer sphere.
b. If a wire is connected between the inner and outer sphere, after electrostatic equilibrium is established how much total charge is on the outer sphere? How much charge is on the outer surface and inner surface of the outer sphere? Does the electric field at the surface of the inside sphere change when the wire is connected?
c. We return to original condition in (a). We now connect the outer sphere to ground with a wire and then disconnect it. How much total charge will be on the outer sphere? How much charge will be on the inner surface and outer surface of the outer sphere?
View SolutionConsider tow concentric conducting spheres of radii a &b(b>a). Inside sphere has a positive charge q1. What charge should be give to the ouer sphere so that potential of the inner sphere becomes zero ? How does the potentila varies between the two spheres & outside ?
View SolutionCapcity of a spherical capacitor is C1 when in sphere is charged and outer sphere is earthed and when inner sphere is earthed and outer sphere charged. Then C1C2 is (a = radius of inner sphere b = radius of outer sphere)
View Solution
