Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
Fig. 460 shows the particles each moving with same speed but in different directions. Consider any two particles having angle between the directions of their velocities.
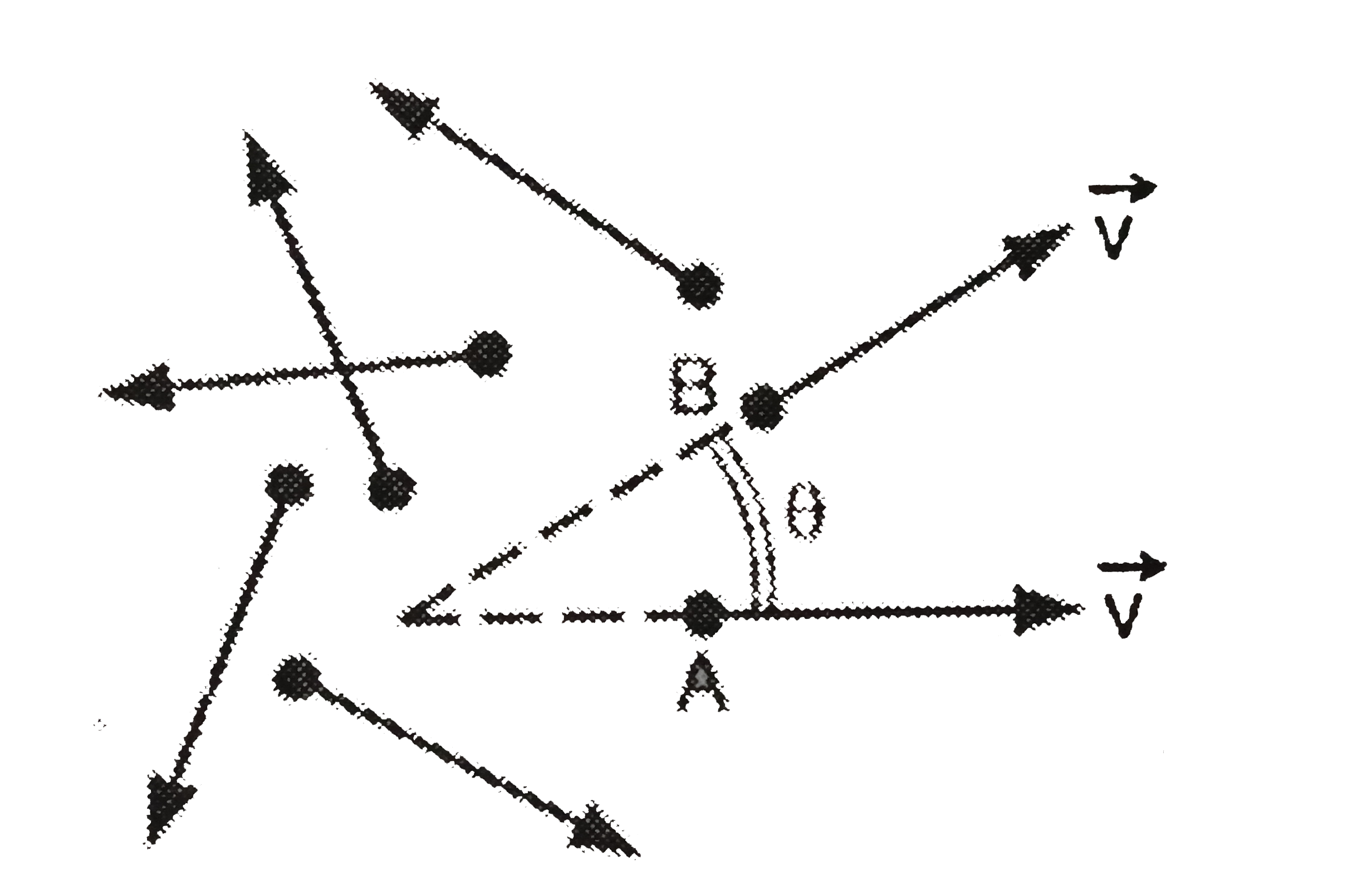
Thus
i.e.,
or
So averaging over all pairs
or [as ]
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Objective question
168 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions
210 Videos
Similar Questions
A particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View Solution
Knowledge Check
Consider a collection of a large number of particles each with speed v in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
A>vB<vC=vDnone of theseA large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
AvB(π/4)vC(4/π)vDZeroTwo bodies are moving in opposite direction with speed V. What is the magnitude of their relative velocity ?
A.0,BV,CY2D2V.
In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :
View SolutionIn a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is:
View SolutionA particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the avergae velocity for its motion form A to
View SolutionThe fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
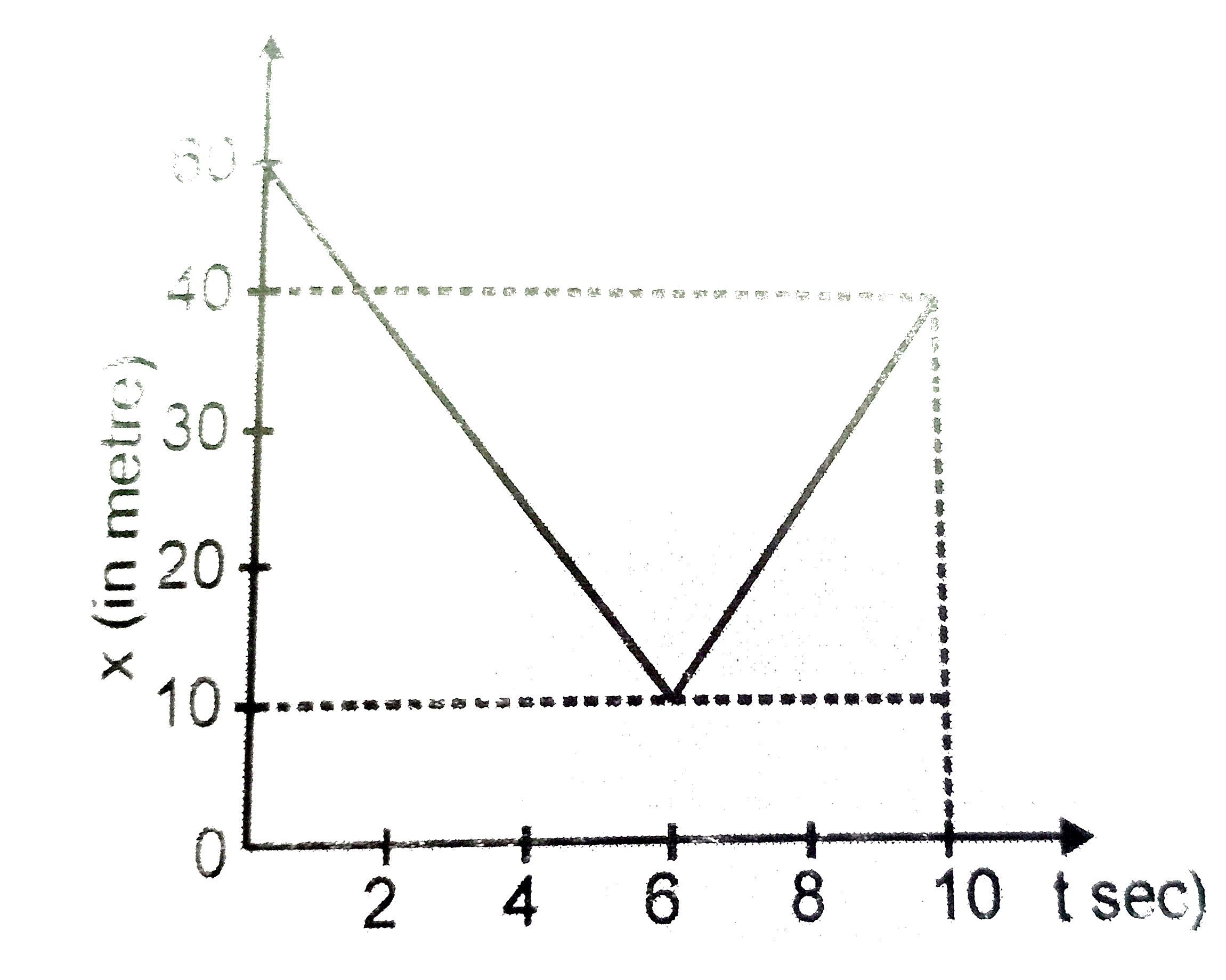
View SolutionAssertion : Particle A is moving Eastwards and particle B Northwards with same speed. Then, velocity of A with respect to B is in South-East direction.
Reason : Relative velocity between them is zero as their speeds are same.
View Solution
