Consider a cycle followed by an engine (figure.)
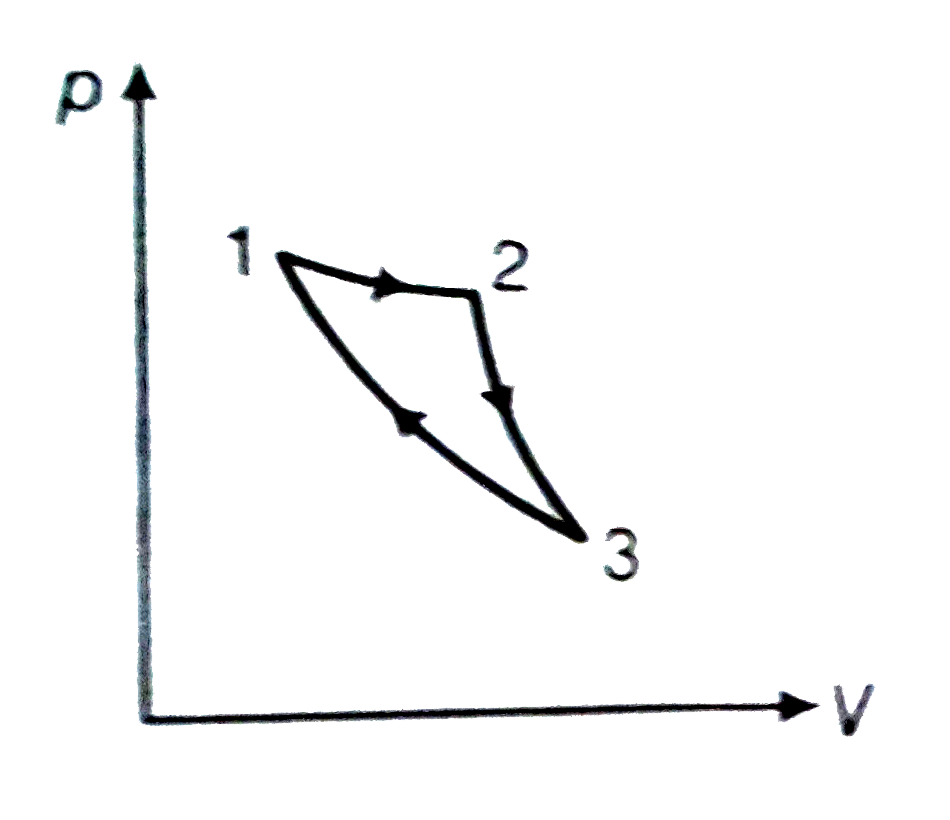
1 or 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
Such a process does not exist, because
heart is completely converted to mechanical energy in such a process, which is not possible
mechanical energy is completely converted to heart in this process, which is not possible
curves representing two adiabatic processes don't intersect
curves representing an adiabatic process and an isothermal process don't intersect
The correct Answer is:A, C
(a) The given process in a cyclic process i.e., it returns to the orignal state 1.
Hence, change in internal energy dU = 0
⇒ dQ=dU+dW=0+dW=dW
Hence, total heat supplied is converted to work done by the gas (mechanical energy) which is not possible by second law of thermodynamics.
(c ) When the gas expands adiabatically form 2 to 3. It is not possible to return to the same state without being heat supplied, hence the process 3 to 1 cannot be adiabatic.
Topper's Solved these Questions
- THERMODYNAMICS BOOK - NCERT EXEMPLARCHAPTER - THERMODYNAMICS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- THERMODYNAMICS BOOK - NCERT EXEMPLARCHAPTER - THERMODYNAMICS EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- THERMODYNAMICS BOOK - NCERT EXEMPLARCHAPTER - THERMODYNAMICS EXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
- UNITS AND MEASUREMENTS BOOK - NCERT EXEMPLARCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions
9 Videos
Similar Questions
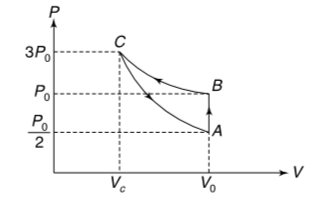
Find work in the given cycle, If AB is isothermal process and CA is adiabatic.
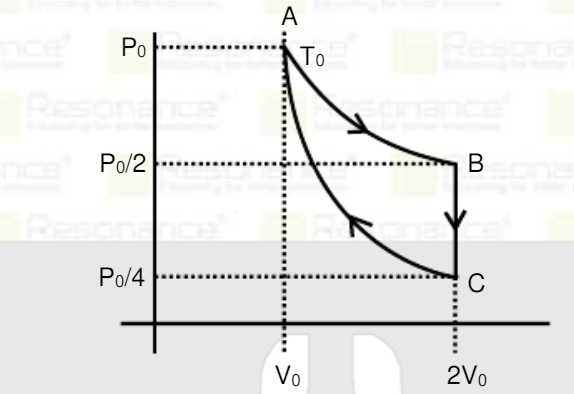
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
View Solution
Knowledge Check
Consider a cycle followed by an engine, (figure)

1 to 2 is isothermal 2 to 3 is adiabatic 3 to 1 is adiabatic
such a process does not exist becauseAheat is completely converted to mechanical energy in such a process, which is not possible.Bmechanical energy is completely converted to heat in this process, which is not possible.Ccurves representing two adiabatic processes don’t intersect.Dcurves representing an adiabatic process and an isothermal process don't intersect.The three processes in a thermodynamic cycle shown in the figure are : Process 1 → 2 is isothermal, Process 2 → 3 is isochoric (volume remains constant), Process 3 → 1 is adiabatic. The total work done by the ideal gas in this cycle is 10 J. The internal energy decreases by 20 J in the isochoric process. The work done by the gas in the adiabatic process is -20 J. The heat added to the system in the isothermal process is
 A0JB10JC20JD30J
A0JB10JC20JD30JAn ideal gas expands from V to 2V in 4 separate processes. Where process 1 is isothermal process 2 is adiabatic, process 3 is free expansion and process 4 is isobaric. If E1,E2,E3 and E4 are the changes in average kinetic energy of the molecules in the isothermal, adiabatic free expansion and isobaric process respectively then choose the correct options.
AE2=E3BE1=E3CE1>E4DE4>E3
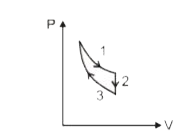
Identify isothermal and adiabatic process in the following diagram
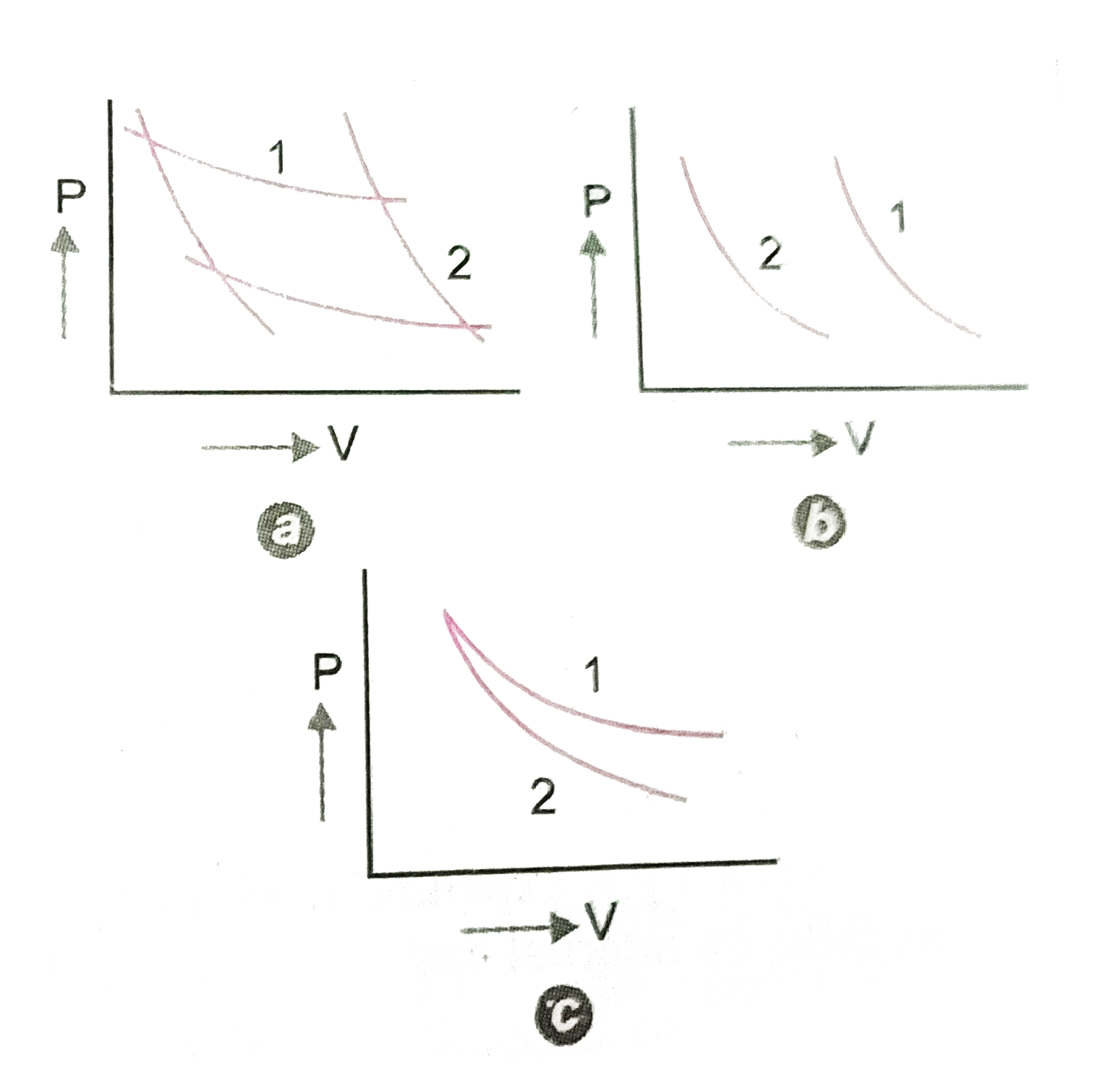
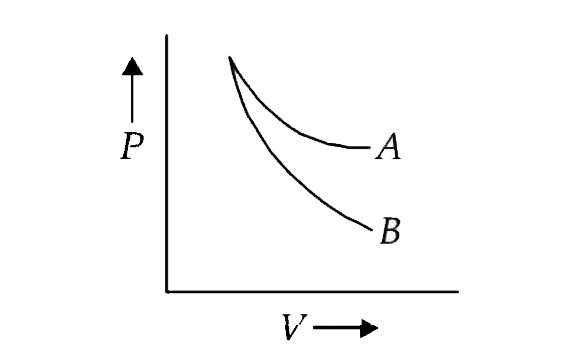
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
View SolutionDefine the following terms :
(i) System
(ii) Isothermal and adiabatic process
View SolutionA heat engine carries one mole of an ideal mono-atomic gas around the cycle as shown in the figure below. Process 1→2 takes place at constant volume, process 2→3 is adiabatic and process 3→1 takes place at constant pressure. Then the amount of heat added in the process 1→2 is
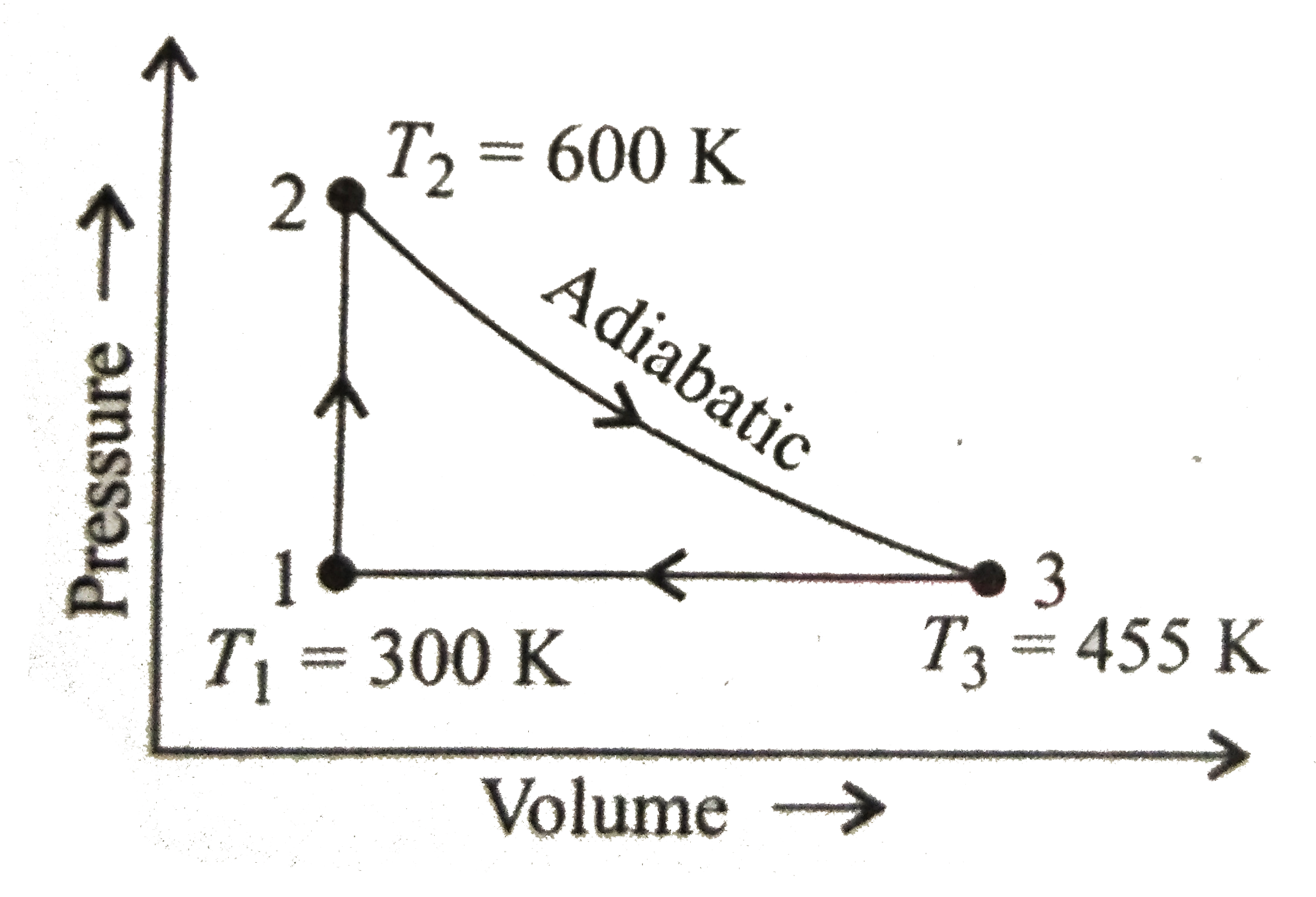
View Solution
