consider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same directioin. The collision starts at t=0 and the particles interact for a time inteval △t. Lduring the collision the speed o the first particle varies as
v(t)=u1+t/v1−u1 Find the speed of the second particle as as function of time during the collision.
Using lw of conservation of momentum m1u1+m2u2=m1v(t)+m2v1
where v=speed of 2nd particle during collision
→m1u1+m2u2
1=m_1u_1+m_1.(t//_\)(v_1-u_1)+m_2v^1<br>rarr (m_2u_20/m_2=m_1/m_2(t//_\t)(v_1-u_1)+v^1<br>: v^1=u_1-m_1/m_2 t//_\t(v_1-u_1)
Topper's Solved these Questions
Similar Questions
A particle of mass 0.1kg moving with an initial speed v collides with another particle of same mass kept at rest. If after collision total energy becomes 0.2J . Then
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then
Speed of the particles after collisionView Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
A0.44B0.5C0.56D0.62 - Question 2 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
A56%B62%C44%D50% - Question 3 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
Adevelopement of air current when the plate is placedBinduction of electrical charge on the plateCshielding of magnetic lines of force as aluminium is a paramagnetic material.Delectromagnetic induction in the aluminium plate giving rise to electromagnetic damping.
Two particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
View SolutionA particle A of mass m and initial velocity v collides with a particle of mass m/2 which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength λAandλB after the collision is
View SolutionTwo particles of masses m1,m2 move with initial velocities u1andu2. On collision , one of the particles get excited to higher level , after absorbing energy ε. If final velocities of particles be v1 and v2 then we must have
View SolutionTwo particles of masses m1 and m2 and velocities u1 and αu1(α≠0) make an elastic head on collision. If the initial kinetic energies of the two particles are equal and m1 comes to rest after collision, then
View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
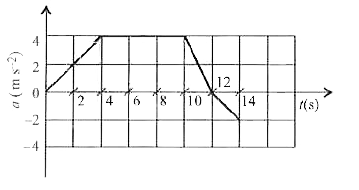
View Solution