Consider a parallel plate capacitor of plate separation d. Each plate has the length l and the width a. A dielectric slab of permittivily $\in$ and thickness d, is partially inserted between the plates. The plates are kept at a constant potential differenc V. If x is the length of the dielectric slab within the plates, determine the force exerted on the slab.

Text Solution

Verified by Experts

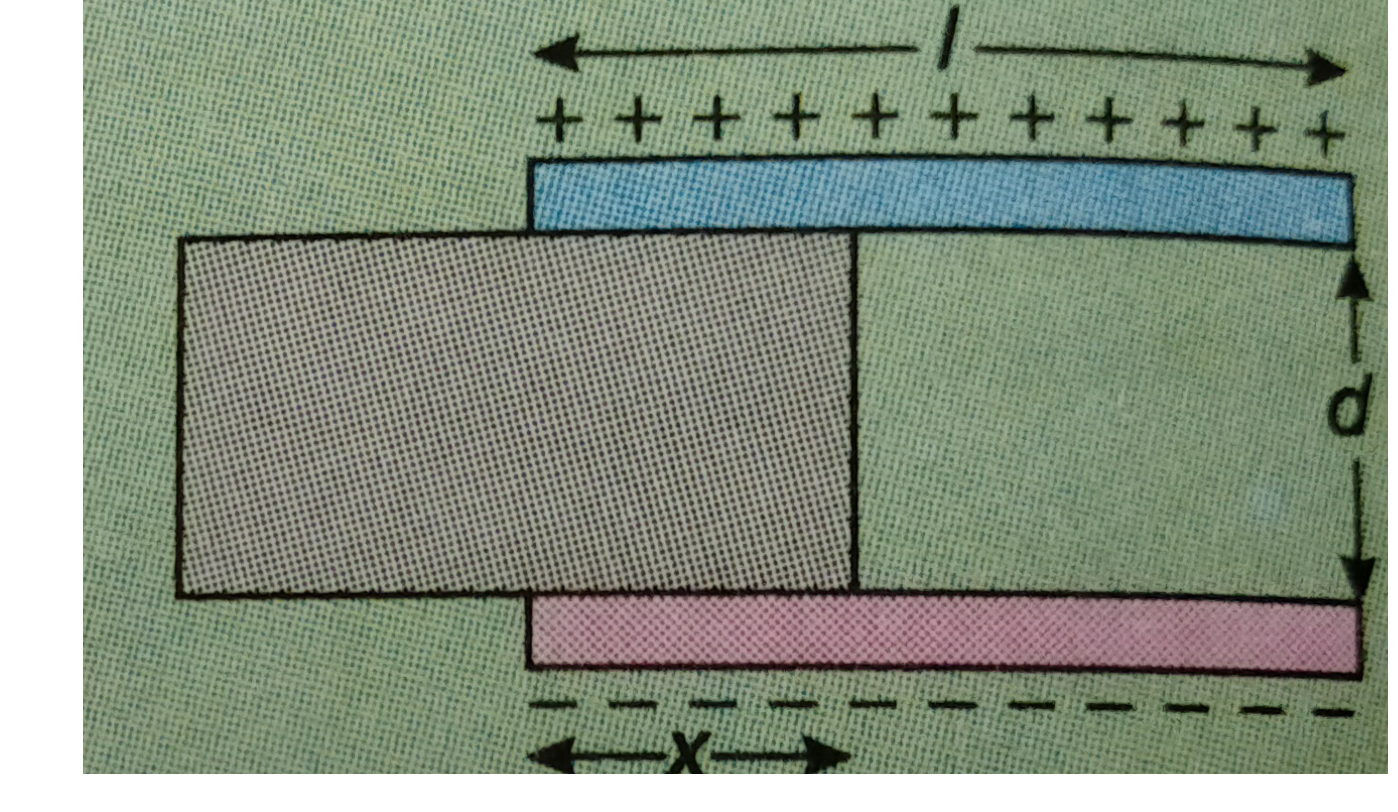
As per the diagram, the system may be regarded as the parallel combination of two capacitances $C_{1} and C_{2}$ . The part containing the dielectric of permittivity $\in$ has capacitance $C_{1}$ and the other part has capacitance $C_{2}$ .
Hence, $C_{1} = \frac{\in a x}{d} and C_{2} = \frac{\in_{0} a (l - x)}{d}$
Equivalent capacitance is, $C = C_{1} + C_{2} = \frac{a}{d} [(\in - \in_{0}) x + \in_{0} l]$
Now electrostanic energy of the system is,
$U = \frac{1}{2} C V^{2} = \frac{1}{2} \frac{a}{d} [(\in - \in_{0}) x + \in_{0} l] V^{2}$
V is constant, the force experienced by the slab is,
$F_{x} = \frac{d U}{d x} = \frac{a}{2 d} (\in - \in_{0}) V^{2}$ .

Updated on:21/07/2023

Separation between the plates of a parallel plate capacitor is $d$ and the area of each plates is $A$ . When a slab of material of dielectric constant $k$ and thickness $t (t < d)$ is introduced between the plates. Its capacitance becomes
A $\frac{ε_{0} A}{d + t (1 - \frac{1}{k})}$
B $\frac{ε_{0} A}{d + t (1 + \frac{1}{k})}$
C $\frac{ε_{0} A}{d - t (1 - \frac{1}{k})}$
D $\frac{ε_{0} A}{d - t (1 + \frac{1}{k})}$
A capacitor with plate separation d is charged to V volts. The battery is disconnected and a dielectric slab of thickness $\frac{d}{2}$ and dielectric constant '2' is inserted between the plates. The potential difference across its terminals becomes
AV
B2 V
C $\frac{4 V}{3}$
D $\frac{3 V}{4}$
Consider an isolated capacitor made of two parallel metallic plate separated by a distance d. the top plate has a surface change density of $- σ$ . A slab of metal of thickness $l < d$ is inserted between the plates. Not touching either plates. Upon insertion of the metal slab, the potential different between the plates
AIncrease
BDecreases
CRemains the same
DBecome zero