Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
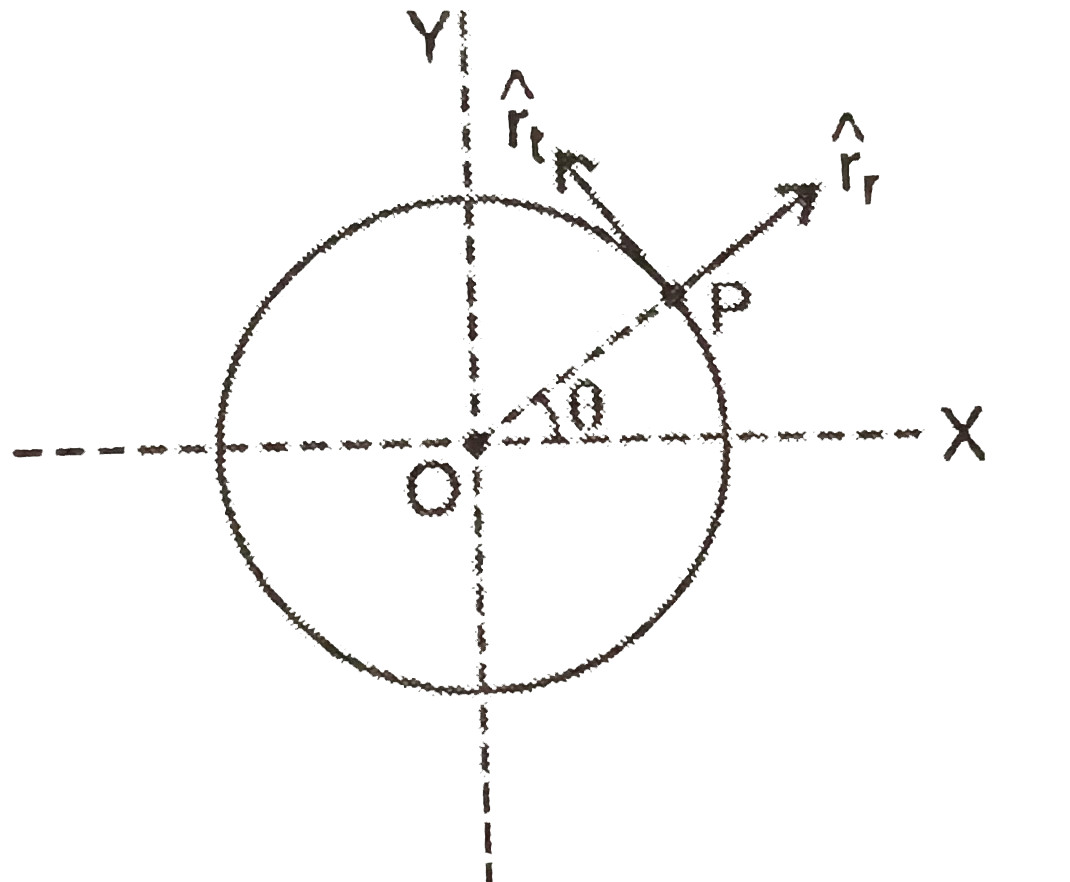
Answer the following questions :
For any position of the objected P, the tangential unit vector can be expressed as :
The correct Answer is:D

→rr=ˆicosθ+ˆjsin(90∘−θ)
=−ˆicos(90∘−θ)+ˆjsin(90∘−θ)
=−ˆisinθ+ˆjcosθ

Topper's Solved these Questions
Similar Questions
Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
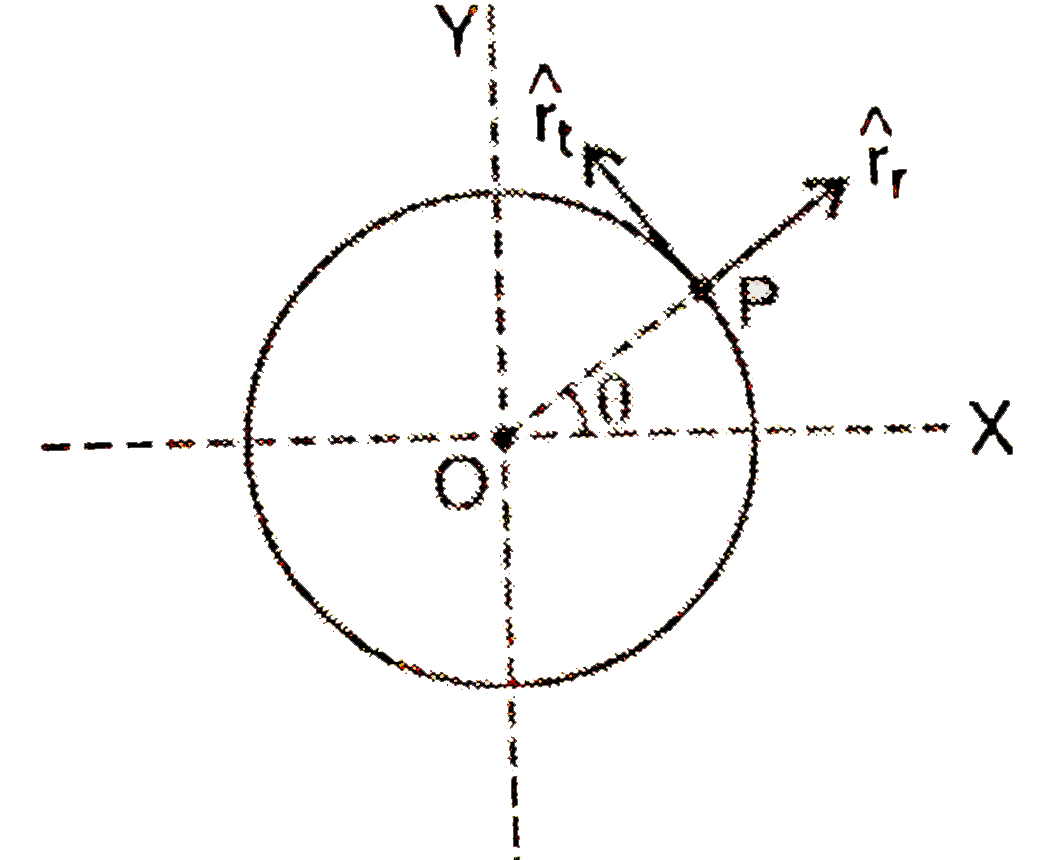
Answer the following questions :
For any instantantaneous position of the objected P, the radial unit vector ˆrr can be expressed as :
View SolutionConsider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.

Answer the following questions :
In trems of ˆrr,ˆrt and θ,ˆi can be expressed as :
View Solution
Knowledge Check
An object of mass 50 kg is moving in a horizontal circle of radius 8 m . If the centripetal force is 40 N, then the kinetic energy of an object will be
A320 jB260 jC220 jD160 jAn object of mass 5 kg is acted upon by a force that varies with position of the object as shown. If the object starts out from rest at a point x=0. What is its speed at x=50 m.
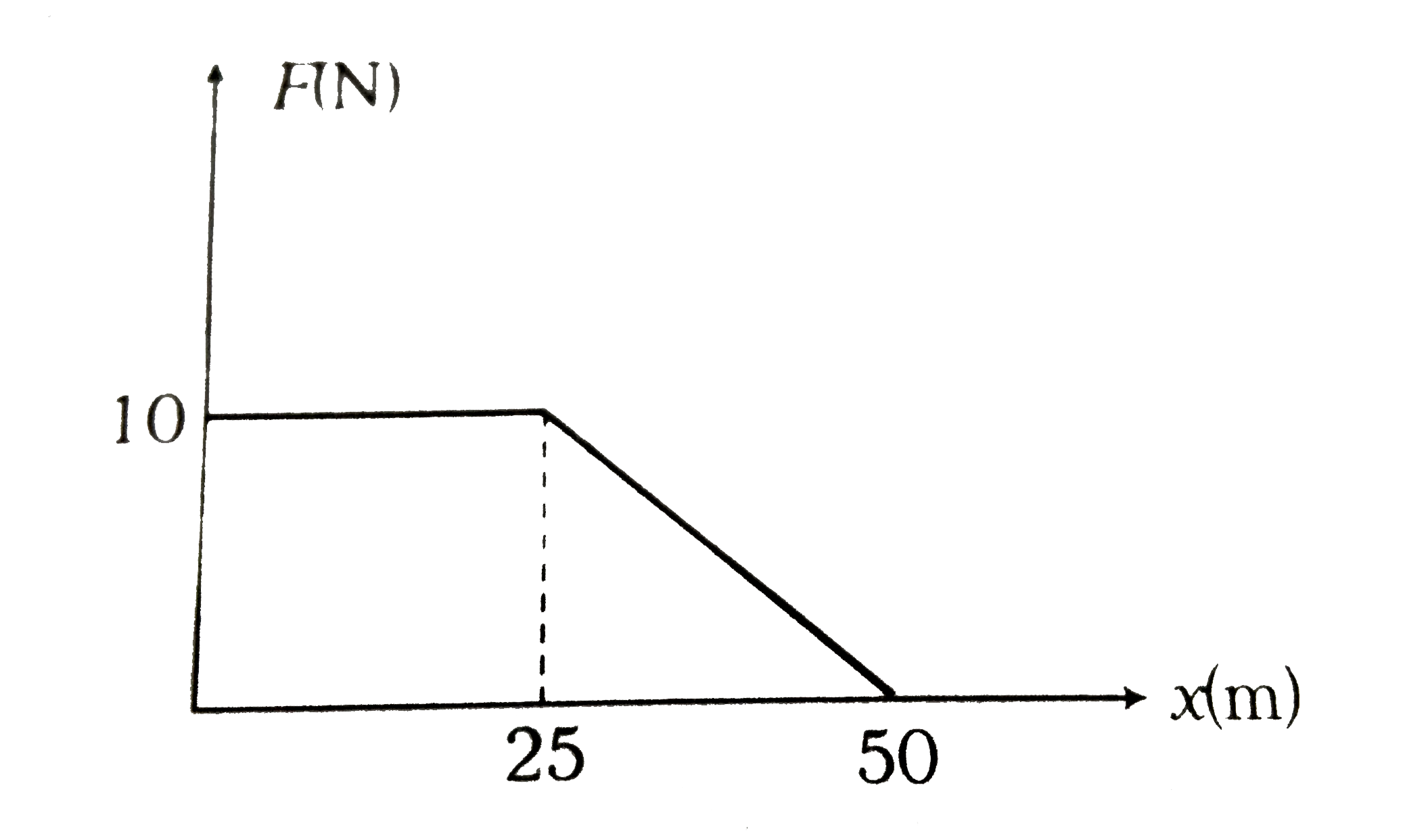 A12.2ms−1B18.2ms−1C16.4ms−1D20.4ms−1
A12.2ms−1B18.2ms−1C16.4ms−1D20.4ms−1The position-time graph of an object moving in a straight line is shown below. The object has zero velocity at
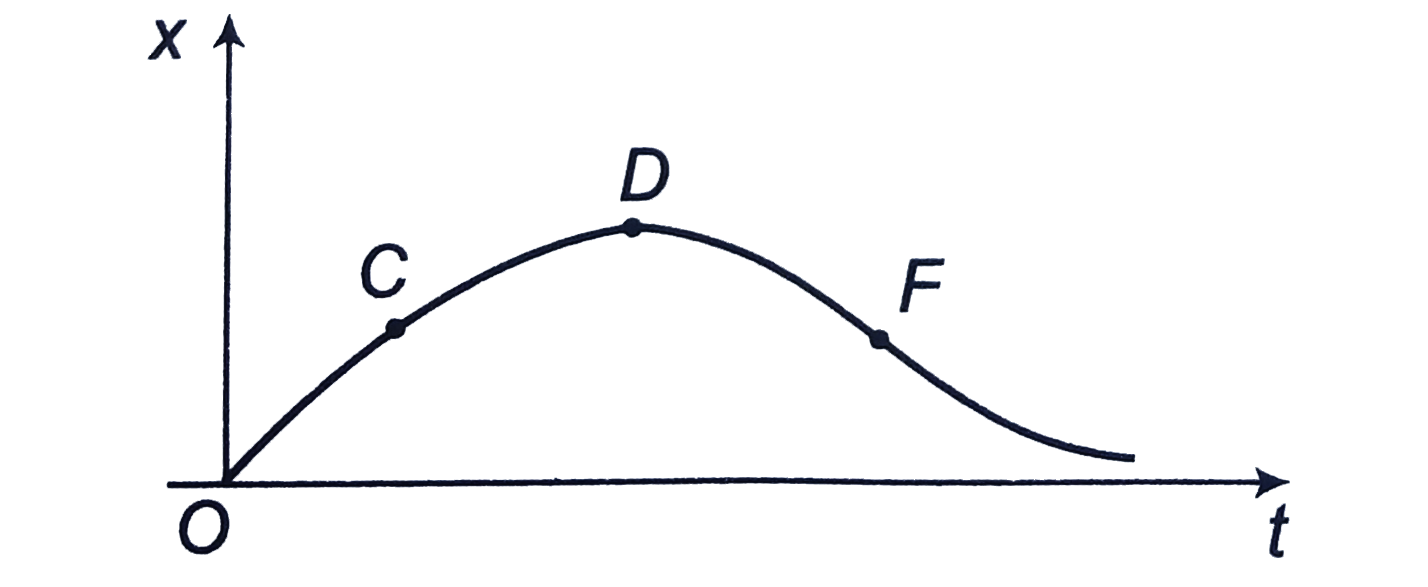 AOBCCDDF
AOBCCDDF
Will the displacement of an object change on shifting the position of origin of the coordinate system ?
View SolutionA particle is moving in a circle of radius 2 m. Show the following position of the particle.
2 m from the centre towards south.
View SolutionAn object of mass 15kg is moving with a uniform velocity of 4m/s. what is the kinetic energy possessed by the object ?
View SolutionAn object of mass m is moving with a constant velocity υ How much work should be done on the object in order to bring the object to rest ?
View SolutionAn object of mass 1 kg is moving with a velocity 10 m/s. Find the kinetic energy of the object
View Solution
