Consider a region of cyclindrical magnetic field, changing with time at the rate x. A triangular conducting loop PQR is placed in the field such that mid point of side PQ coincides with axis of the magnetic field region. PQ = 2l, PR = 2l. Em.f induced in the sides PQ, QR, PR of the loop are

xl2,0,xl2
0,xl22,3xl22
0,xl2,xl2
0,32xl2,xl22
The correct Answer is:C
e=d2l(dBdt)
For PQ, d=0,ePQ=0
For QR, d=l,ePR=l2×2l x=xl2
In close loop, eQP+ePR+eRQ=0
or 0+ePR+eRQ=0∴eRQ=−ePR=eRP=xl2
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 1 : Concept Builder68videos
ELECTROMAGNETIC INDUCTION
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator24videos
ELECTRIC CHARGES AND FIELDS
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator30videos
ELECTROMAGNETIC WAVES
Similar Questions
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
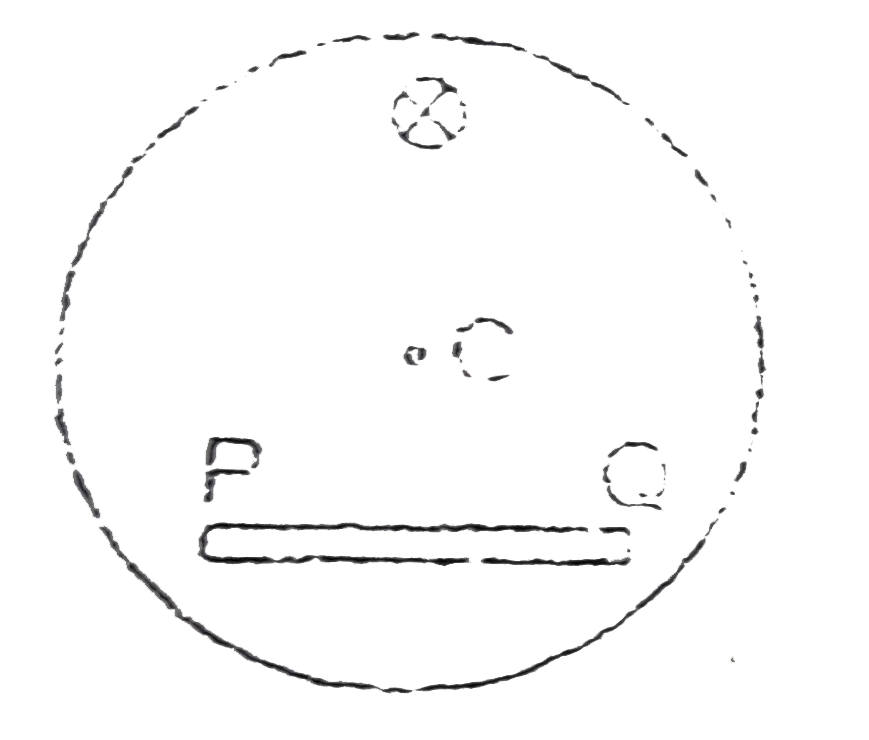
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
A9μ0i4πLB3√3μ0i4πLC2√3μ0iπLD3μ0i4πL - Question 2 - Select One
In a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
 AP will be at higher potential than Q.BQ will be at higher potential than P.CBoth P and Q will be equipotental.Dno emf will be developed across rod as it is not crossing /cutting any line of force.
AP will be at higher potential than Q.BQ will be at higher potential than P.CBoth P and Q will be equipotental.Dno emf will be developed across rod as it is not crossing /cutting any line of force. - Question 3 - Select One
A square non - conducting loop , 20 cm , on a side is placed in a magnetic field . The centre of side AB coincides with the centre of magnetic field . The magnetic field is increasing at the rate 2 T /s . The potential difference betweeen B and C is :
 A30 m VBzeroC10 mVD20 m V
A30 m VBzeroC10 mVD20 m V
A square non - conducting loop , 20 cm , on a side is placed in a magnetic field . The centre of side AB coincides with the centre of magnetic field . The magnetic field is increasing at the rate 2 T /s . The potential difference betweeen B and C is :
 View Solution
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
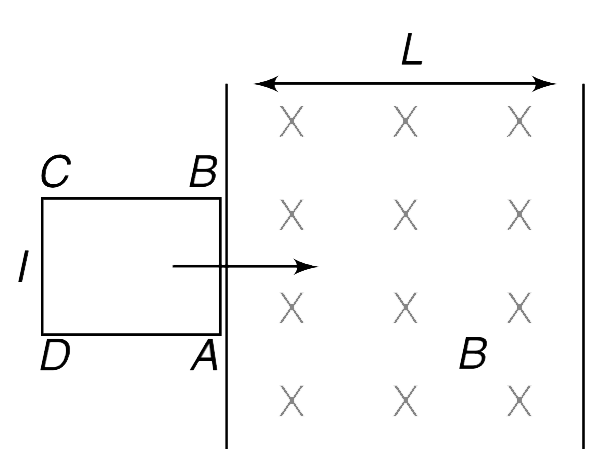
View SolutionA region of width L contains a uniform magnetic field B directed into the plane of the figure. A square conducing loop of side length l(<L) is kept with its side AB at the boundary of the field region (see Figure). The loop is pushed into the field region with a speed such that it just manages to exit the field region. Calculate the time needed for the entire loop to enter the field region after it is pushed. Mass and resistance of the loop is M and R respectively.
 View Solution
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
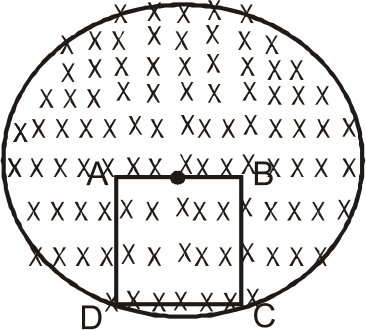 View Solution
View Solution

