Consider a rubber ball freely falling from a height h=4.9m onto a horizontally elastic plate. Assume that the duration of collision is negligible and the collisions with the plate is totally elastic .
Then the velocity as a function of time and the height as a function of time will be :




The correct Answer is:C
v=u+at ∴V=0− gt ∴V=−gt
The down ward direction of velocity of is negative .
After the collision , the velocity is upwards , the upwards motion is a retarded motion . The velocity becomes zero after some time and then it becomes negative . The process is repeated.
S=ut+12at2 ∴h=4.9=0−12>2
This represents a downward parabola.
This represents a downward parabola.
The garph (c) is correct .
If the downward direction is +ve for velocity , then graph (d) is correct.
Topper's Solved these Questions
Similar Questions
A ball falls from a height 20m on to a horizontal plane and rebound to a height of 5/64m after 4 collisions.Find the coefficient of restitution.
View SolutionA ball falls from a height of 5m on to a horizontal plane.If the coefficient of restitution is 0.4, the height to which it rebounds after 2 collisions is approximately
View Solution
Knowledge Check
Consider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
A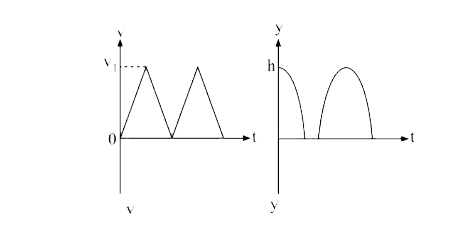 B
B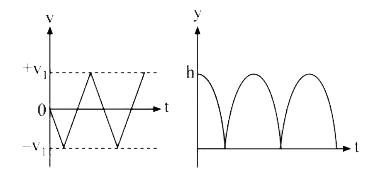 C
C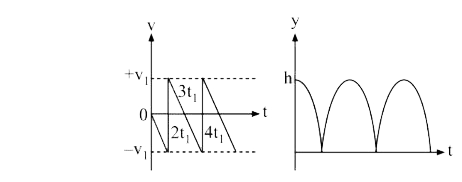 D
D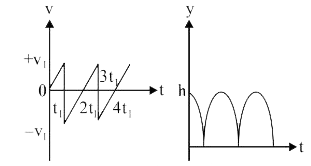
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
A12sB1sC32sD34sA ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
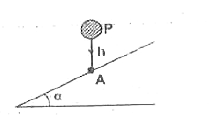 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
A rubber ball dropped from a height of 20m(g=10ms2) falls on the roof of an elevator going up at 2m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of?
View SolutionA rubber ball dropped from a height of 20m (g=10ms2) falls on the roof of an elevator going up at 2m/s .If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of
View SolutionA steel ball of mass 0.5 kg is dropped from a height of 4 m on to a horizontal heavy steel slab. The collision is elastic and the ball rebounds to its original height.
Calculate the impulse delivered to the ball during impact.
View SolutionA ball falls from a height of 10m on to a horizontal plane. If the coefficient of restitution is 0.4, then the velocity with which it rebounds from the plane after second collision is
View SolutionA plastic ball falling from a height 4.9m rebounds number of times. If total time for second collision is 2.4sec, then coefficient of restitution is
View Solution
