Consider a sinusoidal travelling wave shown in figure. The wave velocity is $+ 40 c m / s$ .
Find
(a) the frequency
(b) the phase difference between points $2.5 c m$ apart
( c ) how long it takes for the phase at a given position to
(d) the velocity of a particle at $P$ at the instant shown.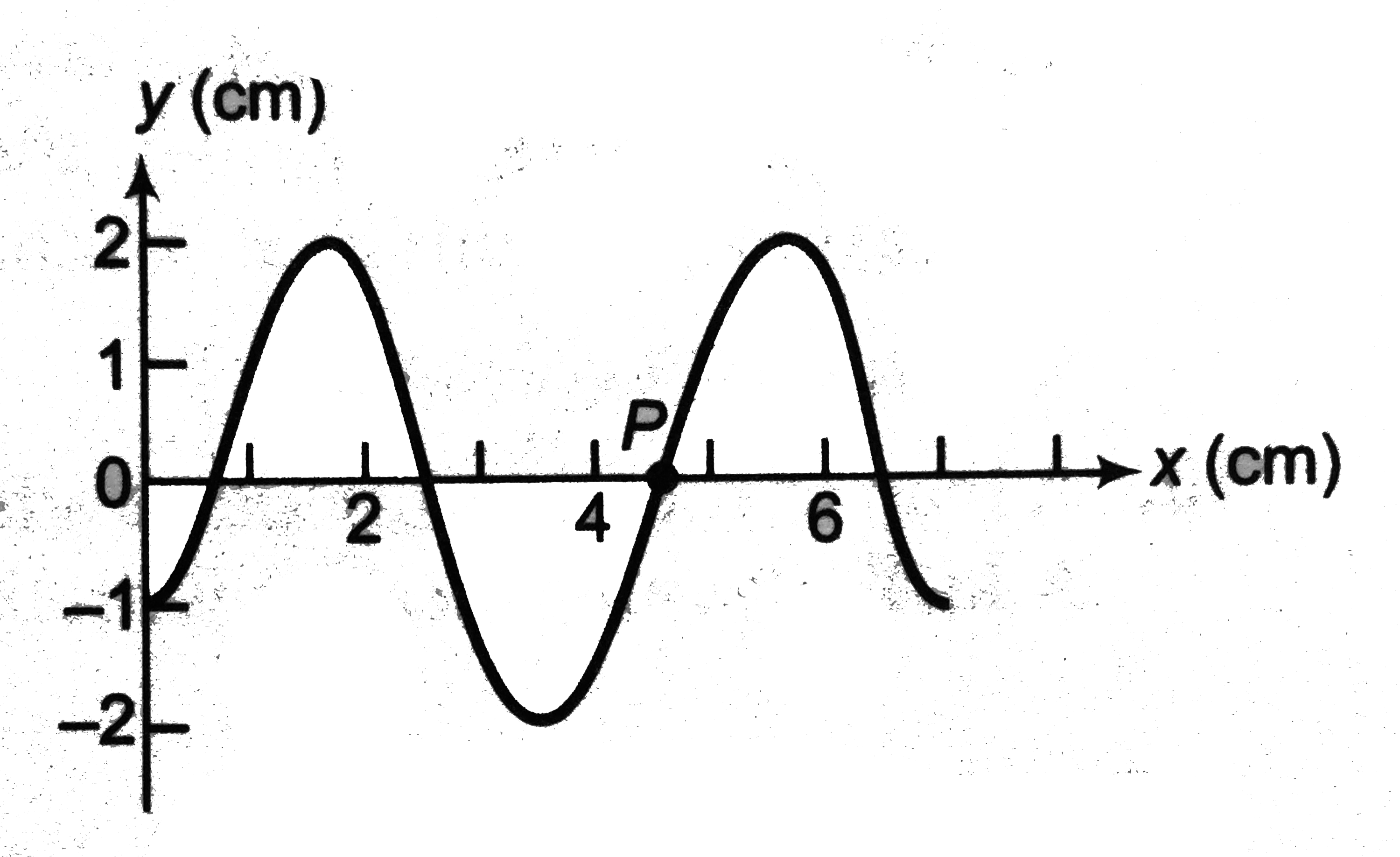

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) $\frac{λ}{2} = 2 c m$
rArr $λ = 4 c m$
$f = \frac{v}{λ} = \frac{40}{4} = 10 H z$
(b) $Δ ϕ = \frac{2 π}{λ} Δ x = (\frac{2 π}{4}) (2.5) = \frac{5 π}{4}$
( c ) $ω t = θ$
or $(2 π / t) = θ$
$∴ t = \frac{θ}{2 π f} = \frac{π / 3}{(2 π) (10)}$
$= \frac{1}{60} s$
(d) At $P$ , particle is at mean position. So,
$v = maximum velocity$
$= ω A$
$= 2 π f A$
$= (2 π) (10) (2)$
$= (40 π) c m / s$
$= 125.7 c m / s = 1.26 m / s$
Further, $v_{P} = - (v) (\frac{\partial y}{\partial x})$ ...(i)
Sign of $v_{1}$ , the wave velocity is given positive.
Sign of $\frac{\partial y}{\partial x}$ , slope of $y - x$ graph is also positive.
Hence, from Eq. (i) particle velocity is negative.
$∴ v_{P} = - 1.26 m / s$

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Small amplitude progressive wave in a stretched string has a speed of $100 c m / s$ and frequency 100 Hz. The phase difference between two points 2.75 cm apart on the string in radians, is
A0
B $11 π / 2$
C $π / 4$
D $3 π / 8$
Question 2 - Select One
The phase difference between two points separated by 0.8 m in a wave of frequency 120 Hz is $90^{\circ}$ . Then the velocity of wave will be
A $182 m / s$
B $360 m / s$
C $710 m / s$
D $384 m / s$
Question 3 - Select One
A transverse wave along a stretched string has a speed of 30 m/s and a frequency of 250 Hz. Then the phase difference between two points on the string 10 cm apart at the same instant is
A0
B $π / 2$ rad
C $5 π / 3$
D $8 π / 3$

DC PANDEY-WAVE MOTION-Level 1 Subjective

Home
Ask Doubt
Profile